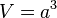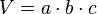Dichte: Unterschied zwischen den Versionen
(→Bestimmung der Dichte von Gasen) |
|||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 51: | Zeile 51: | ||
=== Bestimmung der Dichte von Feststoffen mit unregelmäßiger Form === | === Bestimmung der Dichte von Feststoffen mit unregelmäßiger Form === | ||
| − | |||
| − | |||
| − | + | {| | |
| + | |- | ||
| + | | [[Datei:Waage unregelmaeßigem Koerper.svg|100px]] || | ||
| + | Nehmen wir einmal an, wir vollen von einem Stein die Dichte bestimmen. Für die Berechnung der Dichte brauchen wir von einer bestimmten Portion das Volumen und die Massen. Die Portion hier, ist dieser Stein. | ||
| + | |||
| + | Die Bestimmung der Masse ist einfach: Wir wiegen einfach den Stein. | ||
| + | |||
| + | |- | ||
| + | |<br /> | ||
| + | |- | ||
| + | | <center>[[Datei:Breiter Messzylinder mit blauer Fluessigkeit.svg|50px]]</center> || Das das Volumen des Steins nicht durch Längenmessungen bestimmt werden kann, müssen wir ein anderen Weg wählen. Wir nutzen dazu die Verdrängungsmethode. Dazu geben wir in einen Messzylinder Wasser und bestimmen die Menge an Wasser, also das Volumen. | ||
| + | |- | ||
| + | |<br /> | ||
| + | |- | ||
| + | | <center>[[Datei:Breiter Messzylinder mit blauer Fluessigkeit und unregelmaessigem Koerper.svg|50px]]</center> || Nachdem wir den Stein in das Wasser im Messzylinder gegeben haben bestimmen wir erneut das Volumen, denn der Stein hat Wasser verdrängt und damit ist der Wasserspiegel gestiegen. Aus dem Unterschied der beiden gemessenen Volumina kann man das Volumen des Steines messen. | ||
| + | |||
| + | : ''Übrigens: Natürlich muss man bei der Auswahl des Messzylinders darauf achten, dass der Stein reinpasst!'' | ||
| + | |} | ||
| + | |||
| + | {{AufgabeNr|XX|[[Datei:ARBEITSBLATT Dichte Bestimmung bei Feststoffen als PDF.pdf|100px|right]] | ||
| + | |||
| + | Lade dir das Arbeitsblatt rechts herunter und nutze die Anleitung, um die Dichte eines beliebigen, eigenen Steins zu bestimmen.}} | ||
| + | |||
| + | {{AufgabeNr|XX|[[File:Pyrit-elba_hg.jpg|right|100px]]Mineralien sind gerne gekaufte Andenken. Frage deine Eltern, ob du eines mal für eine Dichtebestimmung nutzen kannst. Damit du dein Ergebnis auch kontrollieren kannst, muss es natürlich rein sein und kein Gestein zusätzlich enthalten. Gehe wieder so vor, wie im Arbeitsblatt beschrieben. Natürlich kannst du dir das Arbeitsblatt auch noch einmal herunterladen und es erneut nutzen. | ||
| + | * Informiere dich vorher bei Wikipedia, ob das Mineral wasserlöslich ist. Wenn ja, dann darfst du die Verdrängungsmethode leider nicht anwenden. | ||
| + | * In dem Wikipedia-Artikel findet du eigentlich immer die Dichte. Vergleiche dann dein Ergebnis mit dem Literatur-Wert. | ||
| + | <small>Das {{wpde|Pyrit|Pyrit}}-Kristall rechts ist nicht wasserlöslich und hat laut Wikipedia eine Dichte von 4,95 bis 5,2 g/cm<sup>3</sup></small>}} | ||
=== Bestimmung der Dichte von Flüssigkeiten === | === Bestimmung der Dichte von Flüssigkeiten === | ||
| + | {| | ||
| + | |- | ||
| + | | <center>[[Datei:Waage_mit_leerem_Messzylinder.svg|100px]]</center> | ||
| + | || Für die Bestimmung der Dichte müssen wir immer das Volumen und das Gewicht einer Stoffportion bestimmen. Beim Stein war die Portion vorgegeben. Bei einer Flüssigkeit kann man eine beliebige Portion nehmen. Da man eine Flüssigkeit nicht alleine wiegen kann, brauch wir erst einmal einen Messzylinder und bestimmen dessen Gewicht, wenn er leer ist. | ||
| + | |- | ||
| + | | || | ||
| + | |- | ||
| + | | <center>[[Datei:Waage mit Messzylinder und gelber Fluessigkeit.svg|100px]]</center> || Dann füllen wir uns erst einmal eine beliebige Menge der Flüssigkeit in den Messzylinder ab und bestimmen das Gewicht des Messzylinders zusammen mit der Flüssigkeit. Aus der Differenz der zwei Werte können wir berechnen, welches Gewicht die ausgewählte Stoffportion hat. | ||
| + | |- | ||
| + | | || | ||
| + | |- | ||
| + | | <center>[[Datei:Kleiner_Messzylinder_und_gelber_Fluessigkeit.svg|50px]]<br /> | ||
| + | [[Datei:Meniskus richtig ablesen - gelbe Fluessigkeit - Skala von Messzylinder.svg|220px]]</center> | ||
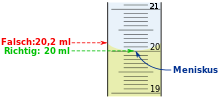
| + | || Das Volumen der Stoffportion kann man leicht an der Skala des Messzylinders abmessen. Achte auf das richtige Ablesen! | ||
| + | |} | ||
| − | {{AufgabeNr|XX|Bestimme die Dichte von Olivenöl}} | + | |
| + | {{AufgabeNr|XX|[[Datei:ARBEITSBLATT Dichte Bestimmung bei Flüssigkeiten als PDF.pdf|100px|right]] | ||
| + | |||
| + | Bestimme die Dichte von Olivenöl. Nutze dazu das Arbeitsblatt rechts, indem du es dir herunterlädst.}} | ||
| + | |||
| + | {{AufgabeNr|XX| | ||
| + | # Bestimme die Dichte von Wasser. Du kannst dazu genauso vorgehen, wie bei der letzten Aufgabe oder du lädst dir noch einmal das Arbeitsblatt herunter. | ||
| + | # Löse dann im Wasser möglichst viel Salz und bestimme dann die Dichte von deinem Salzwasser. | ||
| + | |||
| + | }} | ||
=== Bestimmung der Dichte von Gasen === | === Bestimmung der Dichte von Gasen === | ||
{{AufgabeNr|XX|Nutze eine große Plastikspritze, um die Dichte von Luft zu bestimmen. Ein Anleitung dazu findest du hier.}} | {{AufgabeNr|XX|Nutze eine große Plastikspritze, um die Dichte von Luft zu bestimmen. Ein Anleitung dazu findest du hier.}} | ||
| + | |||
== Aufgaben und Berechnungen mit der Dichte == | == Aufgaben und Berechnungen mit der Dichte == | ||
Aktuelle Version vom 25. Oktober 2015, 14:25 Uhr
Inhaltsverzeichnis |
Worum geht es hier
Wenn etwas im Wasser untergeht sagt man gerne "das war zu schwer". Aber, was ist mit ganzen Baumstämmen? Sind die leicht, weil sie nicht untergehen? Nein, das kann es nicht sein, denn sicher ist ein großer Baumstamm nicht gerade leicht. Und dann geht ja selbst der leichteste Stein im Wasser unter.


Also, damit es ist ganz klar, dass das Gewicht nicht die Eigenschaft sein kann, weswegen etwas schwimmt oder eben untergeht.
Woran liegt es also?
Zunächst einmal sollte man, damit man zwei Stoffe wirklich vergleichen kann, die gleiche Menge davon nehmen. Denn es ist klar, dass wenn man ein große Portion von einem Stoff hat, diese Portion natürlich auch schwerer ist als eine kleinere. Betrachten wir also kleine Würfelchen mit der Seitenlänge von 1 cm, die damit alle das gleiche Volumen von 1cm³ haben. Wiegt man diese Würfel, so stellt man fest, dass die Würfel aus verschiedenen Materialien alle unterschiedlichen Massen haben.
| Stoff | Masse von 1 cm³ |
|---|---|
| Eisen | ??? |
| Aluminium | ??? |
| Holz | ??? |
| usw. | ... |
So zeigt sich deutlich, dass 1 cm³ von Holz wesentlich leichter sind, als etwa 1 cm³ Eisen. Die gleiche Menge Holz ist also leicht als Eisen.
Da man von einem Stoff nicht immer ein 1 cm³-Würfelchen zur Hand hat, müsste man die Masse eines Stoffes mit seinem Volumen vergleichen. Berechnet man den Quotienten aus Masse und Volumen, so erhält man eine Zahl die man als DICHTE bezeichnet.
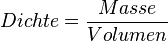 oder mit Symbolen oder mit Symbolen 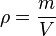 . Einheit der Dichte: . Einheit der Dichte: 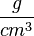
|
- Bei dem "komischen Buchstaben
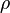 , der fast wie ein "p" aussieht, handelt es sich um einen griechischen Buchstaben, wie ihr sie auch von der Winkelbenennung kennt. Hier ist es das kleine "rho" (lies: roh).
, der fast wie ein "p" aussieht, handelt es sich um einen griechischen Buchstaben, wie ihr sie auch von der Winkelbenennung kennt. Hier ist es das kleine "rho" (lies: roh).
- Bei dem "komischen Buchstaben
Die DICHTE ist ein Staffeigenschaft, mit der sich viele Stoffe unterscheiden lassen. Damit man nicht immer selber die Dichte berechnen muss, gibt es die Werte von ganz vielen Stoffen in Datensammlungen, in denen du nachschlagen kannst. In der Wikipedia findest du zu jeden Stoff, der dort aufgeführt ist, immer auch die Dichte, da es eine wichtige Eigenschaft ist. Einen Überblick liefern die Tabellen hier:
Die Dichte eines Stoffes kann schon helfen, einen Stoff zu identifizieren, daher sollte man auch wissen, wie man die Dichte bei verschiedenen Stoffen bestimmen kann.
Praktische Bestimmung von Dichten
Nicht immer sind Stoffe in praktischen Würfeln oder Quadern gegeben. Bei solchen Würfeln könnte man einfach die Kantenlänge messen und das Volumen daraus berechnen.
Zur Erinnerung:
|
Was aber bei unregelmäßigen Körpern machen, wie etwa einem Stein. Hier kann man das Volumen mit einem Lineal nur schätzen. Oder wie bestimme ich die Dichte von Flüssigkeiten? Denn auch wenn ich aus einer Flüssigkeit kein Würfel herstellen kann, so kann ich den Wert 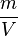 und damit die Dichte berechnen. Und wie sieht es bei Gasen aus?
und damit die Dichte berechnen. Und wie sieht es bei Gasen aus?
Für jeden Aggregatzustand gibt es spezielle Verfahren, wie man die Dichte bestimmen kann.
Bestimmung der Dichte von Feststoffen mit unregelmäßiger Form
|
Lade dir das Arbeitsblatt rechts herunter und nutze die Anleitung, um die Dichte eines beliebigen, eigenen Steins zu bestimmen. |
Mineralien sind gerne gekaufte Andenken. Frage deine Eltern, ob du eines mal für eine Dichtebestimmung nutzen kannst. Damit du dein Ergebnis auch kontrollieren kannst, muss es natürlich rein sein und kein Gestein zusätzlich enthalten. Gehe wieder so vor, wie im Arbeitsblatt beschrieben. Natürlich kannst du dir das Arbeitsblatt auch noch einmal herunterladen und es erneut nutzen.
Das |
Bestimmung der Dichte von Flüssigkeiten
|
Bestimme die Dichte von Olivenöl. Nutze dazu das Arbeitsblatt rechts, indem du es dir herunterlädst. |
|
Bestimmung der Dichte von Gasen
|
Nutze eine große Plastikspritze, um die Dichte von Luft zu bestimmen. Ein Anleitung dazu findest du hier. |
Aufgaben und Berechnungen mit der Dichte
Bedeutung der Dichte für den Auftrieb
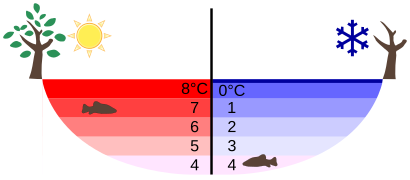
Das Bild rechts zeigt verschiedene flüssige und feste Stoffe übereinander. Von oben nach unten sind es:
- Baby-Öl, rot angefärbter Reinigungsalkohol (Isopropanol), Speise-Öl, Wachs, blau gefärbtes Wasser, Aluminium
Was hat das mit der Dichte zu tun?
Dazu müsste man sich die Dichte-Werte zusammensuchen und die Zahlen miteinander vergleichen.
| Stoff | Dichte |
|---|---|
| Baby-Öl | Beispiel |
| Isopropanol | Beispiel |
| Speise-Öl | Beispiel |
| Wachs | Beispiel |
| Wasser | Beispiel |
| Aluminium | Beispiel |
Du wirst festgestellt haben, dass die Dichte von oben nach unten immer mehr zunimmt.
| Flüssige Stoffe ordnen sich in einem Gefäß immer so an, dass der Stoff mit der geringsten Dichte am weitesten oben ist.
Feste Stoffe können in einer Flüssigkeit ...
Dies gilt natürlich nur, wenn die Stoffe sich nicht vermischen oder ineinander löslich sind. |

|
Und da sind wir eigentlich wieder bei unserer ursprünglichen Frage, nämlich warum Holz auf Wasser schwimmt. Denn die meisten Holzarten (siehe Gleiches gilt auch für die Fettaugen auf der Suppe. Vergleicht man nämlich Wasser und Öl, so hat Öl die geringere Dichte. Oder warst du schon mal im Meer schwimmen? Im Vergleich zu Süßwasser hat das Meerwasser, in dem Salz gelöst ist, eine höhere Dichte und so fällt das Schwimmen im Meer besonders leicht . Das tote Meer enthält sogar soviel Salz, dass man dort gar nicht untergehen kann. Man kann sich bequem hinsetzen und dabei Zeitung lesen. |

|
Wissenwertes rund um die Dichte
Leicht- und Schwermetall
Den Begriff Schwermetalle wirst du vielleicht schon mal gehört haben. Meist wird er im Zusammenhang mit Umweltverschmutzung genannt. Schwermetall-Verbindungen sind meist für den Menschen und Tiere ungesund. Man kann sie allerdings nicht so einfach sehen, die SchwermatellaVerbindungen sind Salzartige Stoffe, die im Wasser löslich sind. Was das mit der Dichte zu tun hat?
Die Begriffe 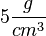 nennt man Leichtmetalle. Darüber sind es Schwermetalle. nennt man Leichtmetalle. Darüber sind es Schwermetalle.
|
Allerdings hat zum Beispiel die recht hohe Dichte von ![]() Blei (11,342 g/cm³) durchaus praktische Anwendungen. Es wird als Gewicht verwendet (Bleigürtel beim Tauchen, Bleiband bei Gardinen) und die schweren Bleischürzen schirmen aufgrund der hohen Dichte auch radioaktive Strahlen ab, weswegen sie beim Röntgen eingesetzt werden. Es gibt zwar noch bessere, weil dichtere Metalle, aber die sind zu teuer.
Blei (11,342 g/cm³) durchaus praktische Anwendungen. Es wird als Gewicht verwendet (Bleigürtel beim Tauchen, Bleiband bei Gardinen) und die schweren Bleischürzen schirmen aufgrund der hohen Dichte auch radioaktive Strahlen ab, weswegen sie beim Röntgen eingesetzt werden. Es gibt zwar noch bessere, weil dichtere Metalle, aber die sind zu teuer.
Auch ![]() Gold hat eine recht hohe Dichte. Und gerade
Gold hat eine recht hohe Dichte. Und gerade ![]() [1] überrascht mit seiner hohen Dichte für eine Flüssigkeit, wenn man das erste Mal eine Quecksilber-Flasche hochhebt.
[1] überrascht mit seiner hohen Dichte für eine Flüssigkeit, wenn man das erste Mal eine Quecksilber-Flasche hochhebt.
Dagegen nutzt man die Leichtmetalle wie ![]() Magnesium und
Magnesium und ![]() Aluminium zum Beispiel beim Fahrzeugbau um Gewicht und damit Treibstoff zu sparen.
Aluminium zum Beispiel beim Fahrzeugbau um Gewicht und damit Treibstoff zu sparen.
Die Dichteanomalie des Wassers
Die Dichte von Wasser ist unnormal!? Das erscheint dir sicher irgendwie merkwürdig, denn Wasser ist ein so alltäglicher Stoff ... wäre einem da etwas Unnormales nicht schon aufgefallen?
Dabei können wir froh sein, dass die Dichte des Wassers, bzw. des festen Wassers also Eis, sich so anders verhält als andere Stoffen. Um besser zu verstehen, was beim Wasser so unnormal ist, solltest du dir diesen Film anschauen:
Folgendes ist zu erkennen:
- Feste Wachsklumpen gehen in flüssigem Wachs unter → die Dichte von festem Wachse ist geringer als die Dichte von flüssigem Wachse
- Gefrorener Eiseissig (= hochkonzentrieter Essig) geht im flüssigen Eisessig ebenfalls unter → die Dichte von festem Eisessig ist geringer als die Dichte von flüssigem Eissessig
- Gefrorenes Wasser, also Eis, schwimmt im flüssigen Wasser → die Dichte von festem Wasser (= Eis) ist höher als die Dichte von flüssigem Wasser
Wachs und Eisessig kann man hier als normale Stoffe sehen. Denn bei allen anderen Stoffen, eben außer dem Wasser, ist es so, dass der feste Stoffe in seinen flüssigen Aggregatzustand untergeht. Und das ist das Unnormale am Wasser.
Wenn man hier mal den Begriff Dichte nutzt kann man also sagen.
| Im festen Aggregatzustand ist die Dichte normalerweise höher als in der Flüssigkeit. |
Wie lässt sich das erklären, dass so normal ist? Im Grunde genommen geht das ganz einfach: dazu müssen wir nur die kleinsten Teilchen von Stoffen betrachten. In dem folgenden Video siehst du eine Simulation eines beliebigen Stoffes und dessen Teilchen bei verschiedenen Temperaturen.
Sortieren wir nun die Beobachtungen ein wenig, indem wir das Teilchenmodell des Stoffes mal in drei einzelnen Bildern betrachten, je eines für jeden Aggregatzustand.
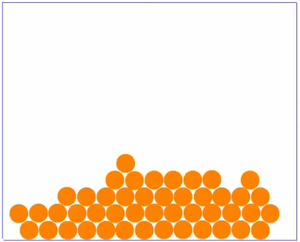 |
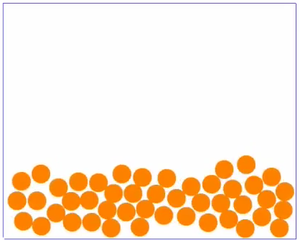 |
 | ||
| Bei sehr niedrigen Temperaturen ist der Stoff fest und ist die Bewegung der Teilchen sehr langsam. Die Teilchen sind ganz nah beieinander und eng gepackt.
Ein Film, bei dem man Teilchen in Bewegung sieht findest du |
Bei mittleren Temperaturen ist der Stoff flüssig sind die Teilchen zwar auch noch nah beieinander, da sich aber die Teilchen mit dem Erhitzen des Stoffes schneller bewegen, können sie nicht mehr eng zusammen bleiben, wie vorher beim festen Stoff. Der von den Teilchen eingenommene Platz ist daher größer.
Ein Film, bei dem man Teilchen in Bewegung sieht findest du |
Bei sehr hohen Temperaturen ist der Stoff gasförmig und die Teilchen sind noch schneller und daher wird ihr Abstand noch größer und die Teilchen sind weit im Raum verteilt.
Ein Film, bei dem man Teilchen in Bewegung sieht findest du |
Aufgrund der Definition der Dichte können wir nun erklären, warum die Dichte dann geringer ist:
- Die Dichte ist ja Masse pro Volumen. Wenn die Masse gleich bleibt (gleich viele Teilchen) aber das Volumen zunimmt (wegen dem Abstand zwischen den Teilchen) dann wird die Dichte beim Erhitzen geringer.
Warum das nun beim Wasser tatsächlich anders ist, lässt sich mit diesem einfachen Teilchenmodell nicht erklären. Auf jeden Fall ist es eben beim Wasser anders als bei den anderen Stoffen, weil Eis eine geringere Dichte als das flüssige Wasser hat. Man spricht deshalb von der Dichteanomalie des Wassers.
Warum ist die Dichteanomalie für uns wichtig?
Die endgültige Erklärung für die Dichteanomalie des Wassers
Wie vorhin erwähnt wurde, lässt sich die Dichteanomalie mit dem einfachen Teilchenmodell nicht erklären. Erklärbar ist sie aber schon, nur sind dazu fortgeschrittene Kenntnisse wichtig. Wer sich es also zutraut, kann sich die folgenden Informationen und Bilder dazu anschauen.
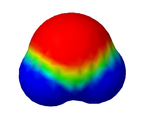
Wichtig ist dazu, dass man weiß, was Wasser genau ist, denn im einfach Teilchenmodell gehen wir ja nur davon aus, dass alle Teilchen aus kleinen Kugeln aufgebaut sind. Aber tatsächlich ist das ja nicht der Fall. Hier nun der Versuch, es auch für Chemie-Anfänger verständlich zu machen.
Was nun diese starke Anziehung zwischen den Wassermolekülen bewirkt, wird im folgenden Video simuliert. Wieder siehst du eine Darstellung des Wassermoleküls wie im letzten Bild.
Zuerst ist die Temperatur etwas höher und wie im einfachen Teilchenmodell sind die Teilchen, also hier die Moleküle, schnell in Bewegung. Mit dem Abkühlen, wenn am Schieberegler rechts oben die Temperatur in der Simulation verringert wird, wird die Bewegung langsamer. Und was dabei passiert, solltest du dir nun mal anschauen.
Die Ansicht wird übrigens hin und wieder gedreht, um sie aus verschiedenen Richtungen betrachten zu können.
Nun, was ist zu sehen? Wie im Bild vorher kann man neben den Molekülen dünne, gestrichelte Linien erkennen, die wieder für die Anziehung der Teilladungen im Wassermolekül stehen. Sind die Wassermoleküle schnell in Bewegung, so ist die Anziehung nicht immer vorhanden, denn dazu müssen die Moleküle einigermaßen nah sein. Je langsamer aber die Teilchen werden, desto besser kann die Anziehung wirken und so sind die dünnen Striche scheinbar "stabiler".
Je langsamer werden desto stabiler wird die Anziehung und man kann schließlich erkennen, dass die Moleküle, auch wenn sie noch in Bewegung sind, eine einigermaßen stabile Position einnehmen. Und diese Position führt gleichzeitig dazu, dass man zwischendurch sechseckige Bereich erkennen kann, die scheinbar immer frei sind. Wenn die Bewegung der Moleküle immer langsamer werden wird das immer deutlicher und schließlich hat man quasi eine perfekte, sechseckige Anordnung der Moleküle.
|
|
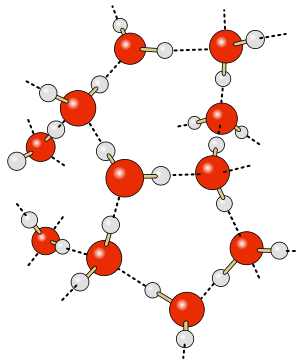
Im Bild links sieht man eine recht große Anzahl an Wassermolekülen. Sie sind regelmäßig angeordnet, was sich ja aus der Anziehung zwischen Wassermolekülen ergibt. Diese starre Anordnung würde es in Realität nicht geben, da die Teilchen auch im gefrorenen Zustand immer ein wenig in Bewegung sind und auf der Stelle schwingen, so wie es in der SImulation auch zu sehen war. Die Wasserstoffbrücken halten die Wassermoleküle aber trotzdem an der Stelle und bewirken die regelmäßige Anordnung.
Die Striche für die Anziehung sind hier noch nicht zu sehen, so können aber sichtbar gemacht werden.
Wenn du dir diese Anordnung von verschiedenen Seite betrachtest, erkennst du eine Struktur, die von einigen Seiten sechseckige Löcher zeigt. WICHTIG: Die hier zu sehende Darstellung, dass die Moleküle einen großen Abstand voneinander haben, ist natürlich alles andere als realistisch. Dieses Kugel-Stab-Modell ist im Prinzip eine andere Darstellung die für die Lewisschreibweise Stäbe und dei Kugeln haben nicht die richtige Größe der Atome. Diese Größe wird im Kalottenmodell besser verdeutlicht (siehe oben).
Nun sieht man, dass sich die Moleküle tatsächlich alle berühren. Man kann kaum zwischen der Bindung zwischen den Atomen und den Wasserstoffbrückenbindungen unterscheiden. Trotzdem sind immer noch Lücken vorhanden! |