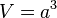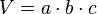Dichte: Unterschied zwischen den Versionen

Aus Chemie digital
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „ Wenn etwas im Wasser untergeht sagt man gerne ''"das war zu schwer"''. Aber, was ist mit ganzen Baumstämmen? Sind die leicht, weil sie ja nicht untergehen? …“)
 
Zeile 1: Zeile 1:
  
  
−
Wenn etwas im Wasser untergeht sagt man gerne ''"das war zu schwer"''. Aber, was ist mit ganzen Baumstämmen? Sind die leicht, weil sie ja nicht untergehen? Nein, das kann es nicht sein, denn sicher ist ein großer Baumstamm nicht leicht. Und dann geht ja selbst der leichteste Stein im Wasser unter.
+
Wenn etwas im Wasser untergeht sagt man gerne ''"das war zu schwer"''. Aber, was ist mit ganzen Baumstämmen? Sind die leicht, weil sie nicht untergehen? Nein, das kann es nicht sein, denn sicher ist ein großer Baumstamm nicht gerade leicht. Und dann geht ja selbst der leichteste Stein im Wasser unter.
 
<center>[[File:Floss.jpg|245px]] [[File:Aberdesach MMB 06.jpg|300px]]</center>
 
<center>[[File:Floss.jpg|245px]] [[File:Aberdesach MMB 06.jpg|300px]]</center>
 
Also, damit es ist ganz klar, dass das Gewicht nicht die Eigenschaft sein kann, weswegen etwas schwimmt oder eben untergeht.  
 
Also, damit es ist ganz klar, dass das Gewicht nicht die Eigenschaft sein kann, weswegen etwas schwimmt oder eben untergeht.  
Zeile 7: Zeile 7:
 
'''Woran liegt es also?'''
 
'''Woran liegt es also?'''
  
−
Zunächst einmal sollte man, damit man zwei Stoffe wirklich vergleichen kann, die gleiche Menge davon nehmen. Betrachten wir also kleine Würfelchen mit der Seitenlänge von 1 cm, die damit alle das gleiche Volumen von 1cm³ haben. Wiegt man diese Würfel, so stellt man fest, dass die Würfel aus verschiedenen Materialien alle unterschiedlichen Massen haben.
+
Zunächst einmal sollte man, damit man zwei Stoffe wirklich vergleichen kann, die gleiche Menge davon nehmen. Denn es ist klar, dass wenn man ein große Portion von einem Stoff hat, diese Portion natürlich auch schwerer ist als eine kleinere. Betrachten wir also kleine Würfelchen mit der Seitenlänge von 1 cm, die damit alle das gleiche Volumen von 1cm³ haben. Wiegt man diese Würfel, so stellt man fest, dass die Würfel aus verschiedenen Materialien alle unterschiedlichen Massen haben.
  
 
{| class="wikitable"
 
{| class="wikitable"
Zeile 20: Zeile 20:
 
|-
 
|-
 
| usw. || ...
 
| usw. || ...
−
 
 
|}
 
|}
 +
 +
So zeigt sich deutlich, dass 1 cm³ von Holz wesentlich leichter sind, als etwa 1 cm³ Eisen. Die gleiche Menge Holz ist also leicht als Eisen.
 +
 +
Da man von einem Stoff nicht immer ein 1 cm³-Würfelchen zur Hand hat, müsste man die Masse eines Stoffes mit seinem Volumen vergleichen. Berechnet man den Quotienten aus Masse und Volumen, so erhält man eine Zahl die man als '''DICHTE''' bezeichnet.
 +
 +
{{Kurzregel|<math>Dichte = \frac{Masse}{Volumen}</math> oder mit Symbolen <math>\rho =\frac{m}{V}</math>. '''Einheit der Dichte:''' <math>\frac{g}{cm^3}</math>}}
 +
:::Bei dem "komischen Buchstaben <math>\rho</math>, der fast wie ein "p" aussieht, handelt es sich um einen griechischen Buchstaben, wie ihr sie auch von der Winkelbenennung kennt. Hier ist es das kleine "rho" ''(lies: roh)''.
 +
 +
Die DICHTE ist ein Staffeigenschaft, mit der sich viele Stoffe unterscheiden lassen. Damit man nicht immer selber die Dichte berechnen muss, gibt es die Werte von ganz vielen Stoffen in Datensammlungen, in denen du nachschlagen kannst.
 +
In der Wikipedia findest du zu jeden Stoff, der dort aufgeführt ist, immer auch die Dichte, da es eine wichtige Eigenschaft ist. Einen Überblick liefern die Tabellen hier:
 +
* [http://de.wikibooks.org/wiki/Tabellensammlung_Chemie/_Dichte_fester_Stoffe Dichte fester Stoffe]
 +
* [http://de.wikibooks.org/wiki/Tabellensammlung_Chemie/_Dichte_fl%C3%BCssiger_Stoffe Dichte flüssiger Stoffe]
 +
* [http://de.wikibooks.org/wiki/Tabellensammlung_Chemie/_Dichte_gasf%C3%B6rmiger_Stoffe Dichte gasförmiger Stoffe]
 +
 +
Die Dichte eines Stoffes kann schon helfen, einen Stoff zu identifizieren, daher sollte man auch wissen, wie man die Dichte bei verschiedenen Stoffen bestimmen kann.
 +
 +
== Praktische Bestimmung von Dichten ==
 +
Nicht immer sind Stoffe in praktischen Würfeln oder Quadern gegeben. Bei solchen Würfeln könnte man einfach die Kantenlänge messen und das Volumen daraus berechnen.
 +
{{Kurzregel|<u>Zur Erinnerung:</u>
 +
* Volumen eines Würfels mit der Seitenlänge a: <math>V = a^3</math>
 +
* Volumen eines Quaders mit den Seitenlängen a, b, c: <math>V = a \cdot b \cdot c</math>}}
 +
 +
''Was aber bei unregelmäßigen Körpern machen, wie etwa einem Stein. Hier kann man das Volumen mit einem Lineal nur schätzen. Oder wie bestimme ich die Dichte von Flüssigkeiten? Denn auch wenn ich aus einer Flüssigkeit kein Würfel herstellen kann, so kann ich den Wert <math>\frac{m}{V}</math> und damit die Dichte berechnen. Und wie sieht es bei Gasen aus?''
 +
 +
Für jeden Aggregatzustand gibt es spezielle Verfahren, wie man die Dichte bestimmen kann.
 +
 +
=== Bestimmung der Dichte von Feststoffen mit unregelmäßiger Form ===
 +
'''Bild, Stein''' Nehmen wir einmal an, wir vollen von dem Kiesel rechts die Dichte bestimmen.
 +
 +
'''Bild, Stein in Messzylinder'''Für die Berechnung der Dichte brauchen wir von einer bestimmten Portion das Volumen und die Massen. Die Portion hier, ist dieser Kieselstein. Die Bestimmung der Masse ist einfach: Wir wiegen einfach den Kieselstein. '''Bild, Stein auf Waage'''
 +
 +
'''Bild, Stein in Messzylinder'''Das das Volumen des Steins nicht durch Längenmessungen bestimmt werden kann, müssen wir ein anderen Weg wählen. Wir nutzen dazu die Verdrängungsmethode.
 +
 +
 +
=== Bestimmung der Dichte von Flüssigkeiten ===

Version vom 13. Dezember 2013, 23:04 Uhr


Wenn etwas im Wasser untergeht sagt man gerne "das war zu schwer". Aber, was ist mit ganzen Baumstämmen? Sind die leicht, weil sie nicht untergehen? Nein, das kann es nicht sein, denn sicher ist ein großer Baumstamm nicht gerade leicht. Und dann geht ja selbst der leichteste Stein im Wasser unter.

Floss.jpg Aberdesach MMB 06.jpg

Also, damit es ist ganz klar, dass das Gewicht nicht die Eigenschaft sein kann, weswegen etwas schwimmt oder eben untergeht.

Woran liegt es also?

Zunächst einmal sollte man, damit man zwei Stoffe wirklich vergleichen kann, die gleiche Menge davon nehmen. Denn es ist klar, dass wenn man ein große Portion von einem Stoff hat, diese Portion natürlich auch schwerer ist als eine kleinere. Betrachten wir also kleine Würfelchen mit der Seitenlänge von 1 cm, die damit alle das gleiche Volumen von 1cm³ haben. Wiegt man diese Würfel, so stellt man fest, dass die Würfel aus verschiedenen Materialien alle unterschiedlichen Massen haben.

Stoff Masse von 1 cm³
Eisen  ???
Aluminium  ???
Holz  ???
usw. ...

So zeigt sich deutlich, dass 1 cm³ von Holz wesentlich leichter sind, als etwa 1 cm³ Eisen. Die gleiche Menge Holz ist also leicht als Eisen.

Da man von einem Stoff nicht immer ein 1 cm³-Würfelchen zur Hand hat, müsste man die Masse eines Stoffes mit seinem Volumen vergleichen. Berechnet man den Quotienten aus Masse und Volumen, so erhält man eine Zahl die man als DICHTE bezeichnet.

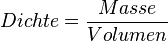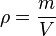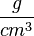
Dichte = \frac{Masse}{Volumen} oder mit Symbolen \rho =\frac{m}{V}. Einheit der Dichte: \frac{g}{cm^3}
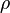Bei dem "komischen Buchstaben \rho, der fast wie ein "p" aussieht, handelt es sich um einen griechischen Buchstaben, wie ihr sie auch von der Winkelbenennung kennt. Hier ist es das kleine "rho" (lies: roh).

Die DICHTE ist ein Staffeigenschaft, mit der sich viele Stoffe unterscheiden lassen. Damit man nicht immer selber die Dichte berechnen muss, gibt es die Werte von ganz vielen Stoffen in Datensammlungen, in denen du nachschlagen kannst. In der Wikipedia findest du zu jeden Stoff, der dort aufgeführt ist, immer auch die Dichte, da es eine wichtige Eigenschaft ist. Einen Überblick liefern die Tabellen hier:

Die Dichte eines Stoffes kann schon helfen, einen Stoff zu identifizieren, daher sollte man auch wissen, wie man die Dichte bei verschiedenen Stoffen bestimmen kann.

Praktische Bestimmung von Dichten

Nicht immer sind Stoffe in praktischen Würfeln oder Quadern gegeben. Bei solchen Würfeln könnte man einfach die Kantenlänge messen und das Volumen daraus berechnen.

Zur Erinnerung:
  • Volumen eines Würfels mit der Seitenlänge a: V = a^3
  • Volumen eines Quaders mit den Seitenlängen a, b, c: V = a \cdot b \cdot c


Was aber bei unregelmäßigen Körpern machen, wie etwa einem Stein. Hier kann man das Volumen mit einem Lineal nur schätzen. Oder wie bestimme ich die Dichte von Flüssigkeiten? Denn auch wenn ich aus einer Flüssigkeit kein Würfel herstellen kann, so kann ich den Wert 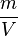\frac{m}{V} und damit die Dichte berechnen. Und wie sieht es bei Gasen aus?

Für jeden Aggregatzustand gibt es spezielle Verfahren, wie man die Dichte bestimmen kann.

Bestimmung der Dichte von Feststoffen mit unregelmäßiger Form

Bild, Stein Nehmen wir einmal an, wir vollen von dem Kiesel rechts die Dichte bestimmen.

Bild, Stein in MesszylinderFür die Berechnung der Dichte brauchen wir von einer bestimmten Portion das Volumen und die Massen. Die Portion hier, ist dieser Kieselstein. Die Bestimmung der Masse ist einfach: Wir wiegen einfach den Kieselstein. Bild, Stein auf Waage

Bild, Stein in MesszylinderDas das Volumen des Steins nicht durch Längenmessungen bestimmt werden kann, müssen wir ein anderen Weg wählen. Wir nutzen dazu die Verdrängungsmethode.


Bestimmung der Dichte von Flüssigkeiten

Von „http://chemie-digital.zum.de/index.php?title=Dichte&oldid=2612“