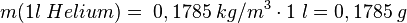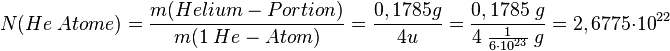Berechnungen von Massen bei Reaktionen: Unterschied zwischen den Versionen

Aus Chemie digital
Wechseln zu: Navigation, Suche
(→‎Stoffmenge)
 
(5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 21: Zeile 21:
  
 
Man legt den Wert fest: '''Molmasse''' (oder '''Molare Masse''') '''M''' mit der Einheit '''g/mol'''.}}
 
Man legt den Wert fest: '''Molmasse''' (oder '''Molare Masse''') '''M''' mit der Einheit '''g/mol'''.}}
 +
 +
{{AufgabeNr|1|Bestimme die Molare Masse der folgenden Stoffe:
 +
* Wasserstoff, Kohlendioxid, ..
 +
{{Lösung|1= Bei allen Rechnungen ist zu beachten, dass man die richtige Formel der Stoffe nimmt. Bei Gasen, die mehratomige Moleküle besitzen, muss man dies beachten.
 +
* Wasserstoff M(H<sub>2</sub>)= 2 g/mol
 +
* Kohlendioxid M(CO<sub>2</sub>)= (12 + 16 * 2) g/mol = 48 g/mol
 +
}}
 +
}}
  
 
== Satz von Avogadro ==
 
== Satz von Avogadro ==
Zeile 49: Zeile 57:
  
 
<ggb_applet width="1100" height="466"  version="4.2" ggbBase64="UEsDBBQACAgIANNZdEIAAAAAAAAAAAAAAAASAAAAZ2VvZ2VicmFfbWFjcm8ueG1s7VbNTtwwED7DU1g+UbXkZxeqCm1AArUCqUAlOFS9TZwhcXHsKPayuzxYX6AvVv8kS3YRLUUcSsUevBN7/r5vZpxMDua1IDfYaq5kRtMooQQlUwWXZUan5mr7Az3Y35yUqErMWyBXqq3BZHQnGtE7O/sUjXadMZlrvifVGdSoG2B4wSqs4bNiYLxmZUyzF8ez2SzqfUaqLeOyNNFcF5TYfKTOaCfsWXcrRrOxVx8lSRp/Pf0c3G9zqQ1IhpTYXGtgrSKsLlwSGf3I5S2KHMQ1SkqMUuKh/WMUjYvMmZKfuEAn60rNTuSlPT2ENqOmndogTDWLI2gcIt3t9XFPZDM1BJKMHiusrC6kGf0GlbDSKKOHPlz184c9inub86npjcK5P7JJaOuauSjEcBPygampVOukAozbsZoosEZpiFk0dkdOa2w5o0RAjmI15P7mxuQGxBSJXTOaRGMXamPiUBKVf0dmS3sFQuPS3KPzSvb8SAnVEhveVrr0a+5XEE0Fzl8aVAUssO1i9DvW26kqusidHkhe+8Yg2mDjtoluEAsvBTjWe2Pd+X4MmTly4g7zH9GHKqzhTl2r/ufAfc+t4T6Ds5cPm6m6BlkQ6af4ixKLUkmPlC9nbyt5R3zlyVsy6P83YRzvTrfXT+2IbjnmHlQYryms+Q/E3ZtnHxaC/zx4sZWCnYwWAV4H6l5Vmw7e6jB7tIJLvDALgcRUnF1L1PYuGg1odMIxLwqUS/5X6h7uss7xkurVuqe7Y1/53fTJpU9+37caS/e0TATocyea/E2iG7a/VFtoMnem75PhL92hZBE8ktuh5ydUwvaIcE1+Io19iaK/5XXIY4DwGrG5tMbn8rIFqd3LN+j0U/p4XvN/h1d3DTki/f/t4Fp6EUSyVyKfh8jilcjHEhkPPwbds/9udEL/Eb3/C1BLBwg11vtItgIAAMoLAABQSwMEFAAICAgA01l0QgAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK4FAFBLBwjWN725GQAAABcAAABQSwMEFAAICAgA01l0QgAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWztXety2zYW/p0+BUY/dtquLBPgVVk7ndghk87kNnG2s9NMf1AiLKGmSIWkfMn0cfYJ+mMfoH2xPQAIihItmYzsUCnrJAZBHlzO+c75AB5RzNEP17MQXdIkZXF03MMDrYdoNI4DFk2Oe4vs/MDp/fDkm6MJjSd0lPjoPE5mfnbcMwakt2wHtQExeWMWHPccR6PBcBgc2DrVDgyDBgeOcR4cGL5pG2N6ToeU9hC6TtnjKH7tz2g698f0bDylM/9lPPYz0ec0y+aPDw+vrq4GavRBnEwOJ5PR4DoNeghmHqXHvfzgMXS30uhKF+JE0/Dhf169lN0fsCjN/GgM43OtFuzJN4+OrlgUxFfoigXZFGyAsdlDU8omU9DT0kCpQy41B2XndJyxS5pC21JVKJ3N5j0h5kf8+iN5hMJCnx4K2CULaHLc0wYmNuyhQzSL2I5GrGEPxQmjUZbL4nzMQ9Xb0SWjV7JbfiRGNLShDRiwlI1Cetw798MU1GLReQImhQklC6im2U1IR36i6sv54D78AQH2ifK+QE1ph+MeIaSPMenbmtY3zVz/0sBOD2VxHIpeMZgX/YagILLQEfpNHJiybuRVS1ZtUWBNFji/6PBfQ16xtmiU17eppCuF9LJC0Hmf/wMw+4ZWVQiXBpV9bh4zP1EaVA1pYqv+kEbJhhoyhe5EIxrq8wLLgkBhWfKSJs+BfUVBZGHIwpQyhmxuSFFDyhhSxtAbKLlu2MKsEMD1dSQNvLNi1mJIUkZyqFl9nQz7xNyAZCP/2YwlNkuDwljir/hXGVLfpubdLvsZI1rGLmH/GQPa2pcY8OhQkdxRHhoonXLZ3FszOkt5sOhDES8IIxOCwrLBvU2Eh1DYnIMIwiYyTKhiB1m8tJHOacdAOnIQl8M6ElFhOvDLEJRkIRP64idtyU1IN5CpIyxiyUAQQUjEI8Qm0UHCNJEJjfjomA+rW8iwoKI7yIAJ8ki0OTPq0A7qMDhBOkY6b4ttRCxkEWTzaMYGD3LL4XOHTgmyNGTxphDOEMoyjKGFg3SuTU6kQAg9NI9TVlh5SsN5AY8wKIvmi2zFiONZoA6zeE06iMcXJ2tGp36aqWMQggVpuezJBWplVXx0FPojGsLm4Yz7A0KXfshDWfR/HkcZUr5A5LlJ4s+nbJye0SyDVin61b/0X/oZvfZAOlUTFEOL1fqILsYhC5gf/QTOwrvgHSK1eAsOVmu3YZlylHEcJ8HZTQoehK5/pknM1/UBNyGsS5ZtWpYJK/CNvGJgezAs/TicicY+d31TH2iOrhFDNx3LsR0w+k1+iVgD09GXPyQfml4WqvnXNFW2nCQ8rnLr88qP6UkcLk/NYxZlp/48WyRiJwZzSLhST6NJSIVtBb3CnmZ8MYqvz6RRddnX+5s51DQ5gdHkNA7jBEFkEhM2NpO8HMlSyPCZFVKakNGEhKZQYkFxHQ+JkBDlSJZCCmCXU8s11ZWaWFPDsFTwCXRedjLhM3yDtIhY9lJWvsfaH7//8Tu4KRtf5ArnzV4vZiPwusKPQeAZk7u6fAcrw+KSPoUBc7HVCeC7J7AyMlkbueSVa/54lM4T6gfplNLsdg/lK2jhobojZwaNzk9pGJ6VRTntKkk8lIKl7gGRxSxSBs3bOFvlcCFnadvkyFLO2ianF3LYwNsEjUJwuHVgc9mhoojbBa2SoF0RfBdfKbsoAxJlGBpyuoojhKZn4yQOQyF2WToei2GEFRK5z8kd3L+JF5zCwBU8uA9ahP5JaRvBTz8XDp8viVB/Ibs9WS6M/OxPpbOlxicwWkqTt7DnD1cuSL1fgHZ0tQXoKc+i4rQfhvHVGVAy80M3YFmcrF56D0vrezYvwod+XMDVd1CwhC4JyF9k8Wk8m4c0oyV/X4UDHNYT94Movy985cOaovW1/rh/gC0b46Fu9c/7+DG59RyGkjw25DXLNPMLRn7Bggu8buV1Ezro+33tsa4O8PKg2r+eN9NvuWauj2mpngx1QNSBlh/IeK/E99EFTQAwuc5EQPWLeJHKha9ktkVK3/rZ9GkUvKMT8L63Pt89ZcAmUnRJUgFAN4OG8rxiaM77/wZ2kmcDOkmoIrVQ3BtL5hVXtfKqVzktuvKSePZjdPkeFpW1qR4dKn2O0nHC5nztQiPYzl2UvCNgqQ+bwaDcDpRPQQsZWxnLOG8KP5pyF4Q2fiZ28+jVn/9NPsF+CpYrvp5fg0FTnkZQNPwUWArOHvf+8XERZ/86y+Lzc3koxoH4ncGdMsrEKgc7haxXailcFCIDxaNfIc6Xe3wpUUIEBDaseRAo86nPb9Ora6i2soIuZYu1FEgCwrFscDH0qzgowwDrhlTjVgucrFngZjaKw3omOHkgE9yHWqeraj1j42lG66l1usdqPVtV62kWzw4O31MWwu4smvlpSuFmCS3qKfpsjxV9qq8o+gI2+otZzcjU21QL7j3YNQ1WmfaOEFzXtWb47bmeKzOPFjOasPEyyOTkofVC9TrAtpMT2xadlotXHZVwTZXwRpVgEVtcs5D5yU0TTE/JCqYQlJPDmrQKTdvFld87w96QnS/3f3Cr8Ip3ZasEy4GR52Hq0VbFGnUp6q9nC3eVwmffYhR+V88a7v4Q9tbgflYJbkMN9fVHtluN7JroterLdyilliDgZVTVYx1gdyt7N5j7/cHire2Mok/+NERqa1QPIe/h9/QqL7Yue697ek+h6eroED3T0ffIXMkzwo/pklpQexWoycCybaPUleUS0jhw7w/555WAlPm8epg/3+OofK5w9DiOeKBxQ9fA7PndmDltAnYPofr86wzVrbCd+OEFjaZ//m9Kq/Sqt7t++hGbiQ/ZYKdD5zKrPadU5nmz/EMANIfuxGcI5aR1Te1fxLSqN2573/Dwev8Mzl8N15ZvhL4A3KTq418p1vVocPvtsL1ujdf+67+yNao7UFvtQO1aO9DNBvsS28/ttz+dB9NTYLo234DasAG1+O6l3o5zN2jvf7uilPHsZruwdvXYzjdO113UdRTfOLX4ZrPB2uebzoPpKTBdh/ON04xvdoP2/vlGKeM5zfimXT22882w6y7qDhXfDGvxzWaDtc83+w8m7+BhGUfB6Q454wybMc5u4N4/4yhlvGEzxmlXj+2Mg/Hee+lDUw5WiTZujDqks8Vm7bPO34B6BaCAFKcd+N2Id3bE9wEywUohTyjUgHpaVuUO7tG67qoumEBxj1aPezbbbA+4p/OAegWggJTgHq0h9+yG7wNwj1Zwj9aQe9pV5Q7uqSTWu+aqLiYF99QC1N1isz3gns4D6hWAAlKCe0hD7tkN3wfgHlJwD2nIPe2qsjI58c2xYmpv7vpE/m6XFB+53+PzqBt1yr+xkKJrORC6yctPpc+chXriW1KirV4+u/ZVh/rh/OaWR6c6/Lnnm78/Bl5ZvCve0TWud3HxKCKu9yziFpvtweLdeUC9AlBASizeesPFezd8H3i3bXQdXxdMoALWqBewm222BwHbeUC9AlBASgSs0TBgd8P3gQPW7Dq+Ln/nVB6wZr2A3WyzPQjYzgPqFYACUiJgzYYBuxu+DxywVtfxdfmLZvKAteoF7Gab7UHAdh5QrwAUkBIBazUM2N3wfeCA7fzjry4uHmbG9Z5m3mKzPQjYzgPqFYACUiJgGz7SvCO+OwbsOJ7N/ChAkXiJ3hn9uKD8taS8tXxtm68d997T6+wDf83OB9JHDP0TkV/66NsDbWDz6gGCWXz3C8wJH/cYFESY2tf5u/ZyRRZZuS8vDif5TPLxK2YKWbpMHy/bVBxL6NTge11EMz4/jbx8tVg2ZeOLCDxBvJ6p8Cp+8IIFAY0Kd6yXKT7AnwWMy6JPNByJL4d9YH0kMLKXGJW+NlYXH9kkYP4k8WezBiCtNbxnpOqSQAtI3bHmdT5p4BZJoHo5oH1OAXUeTK9IAIn8T8P0zz5nfzqfK3CL3E+91M8+Z346D6ZX5H1E2qdh1mefkz6dTxG4RcqnXsZnnxM+nQfTK9I9ItvTMNnTbq6n+uyS2hx4RrMnl9rdF1T1UOTpmc30aJc3q3oo5/KsZnrsm18Vzwl4uOHrblp+QuAWVYoYwQ2DpOXPTm9RpQgT3DBOWv5U6RZVikjBDUOl5Xz7LaoU7yTADV9K0G4m8rD85mZeV//d0pP/A1BLBwhm/xw2JgwAAB5qAABQSwECFAAUAAgICADTWXRCNdb7SLYCAADKCwAAEgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfbWFjcm8ueG1sUEsBAhQAFAAICAgA01l0QtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAA9gIAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADTWXRCZv8cNiYMAAAeagAADAAAAAAAAAAAAAAAAABTAwAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAvgAAALMPAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 
<ggb_applet width="1100" height="466"  version="4.2" ggbBase64="UEsDBBQACAgIANNZdEIAAAAAAAAAAAAAAAASAAAAZ2VvZ2VicmFfbWFjcm8ueG1s7VbNTtwwED7DU1g+UbXkZxeqCm1AArUCqUAlOFS9TZwhcXHsKPayuzxYX6AvVv8kS3YRLUUcSsUevBN7/r5vZpxMDua1IDfYaq5kRtMooQQlUwWXZUan5mr7Az3Y35yUqErMWyBXqq3BZHQnGtE7O/sUjXadMZlrvifVGdSoG2B4wSqs4bNiYLxmZUyzF8ez2SzqfUaqLeOyNNFcF5TYfKTOaCfsWXcrRrOxVx8lSRp/Pf0c3G9zqQ1IhpTYXGtgrSKsLlwSGf3I5S2KHMQ1SkqMUuKh/WMUjYvMmZKfuEAn60rNTuSlPT2ENqOmndogTDWLI2gcIt3t9XFPZDM1BJKMHiusrC6kGf0GlbDSKKOHPlz184c9inub86npjcK5P7JJaOuauSjEcBPygampVOukAozbsZoosEZpiFk0dkdOa2w5o0RAjmI15P7mxuQGxBSJXTOaRGMXamPiUBKVf0dmS3sFQuPS3KPzSvb8SAnVEhveVrr0a+5XEE0Fzl8aVAUssO1i9DvW26kqusidHkhe+8Yg2mDjtoluEAsvBTjWe2Pd+X4MmTly4g7zH9GHKqzhTl2r/ufAfc+t4T6Ds5cPm6m6BlkQ6af4ixKLUkmPlC9nbyt5R3zlyVsy6P83YRzvTrfXT+2IbjnmHlQYryms+Q/E3ZtnHxaC/zx4sZWCnYwWAV4H6l5Vmw7e6jB7tIJLvDALgcRUnF1L1PYuGg1odMIxLwqUS/5X6h7uss7xkurVuqe7Y1/53fTJpU9+37caS/e0TATocyea/E2iG7a/VFtoMnem75PhL92hZBE8ktuh5ydUwvaIcE1+Io19iaK/5XXIY4DwGrG5tMbn8rIFqd3LN+j0U/p4XvN/h1d3DTki/f/t4Fp6EUSyVyKfh8jilcjHEhkPPwbds/9udEL/Eb3/C1BLBwg11vtItgIAAMoLAABQSwMEFAAICAgA01l0QgAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK4FAFBLBwjWN725GQAAABcAAABQSwMEFAAICAgA01l0QgAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWztXety2zYW/p0+BUY/dtquLBPgVVk7ndghk87kNnG2s9NMf1AiLKGmSIWkfMn0cfYJ+mMfoH2xPQAIihItmYzsUCnrJAZBHlzO+c75AB5RzNEP17MQXdIkZXF03MMDrYdoNI4DFk2Oe4vs/MDp/fDkm6MJjSd0lPjoPE5mfnbcMwakt2wHtQExeWMWHPccR6PBcBgc2DrVDgyDBgeOcR4cGL5pG2N6ToeU9hC6TtnjKH7tz2g698f0bDylM/9lPPYz0ec0y+aPDw+vrq4GavRBnEwOJ5PR4DoNeghmHqXHvfzgMXS30uhKF+JE0/Dhf169lN0fsCjN/GgM43OtFuzJN4+OrlgUxFfoigXZFGyAsdlDU8omU9DT0kCpQy41B2XndJyxS5pC21JVKJ3N5j0h5kf8+iN5hMJCnx4K2CULaHLc0wYmNuyhQzSL2I5GrGEPxQmjUZbL4nzMQ9Xb0SWjV7JbfiRGNLShDRiwlI1Cetw798MU1GLReQImhQklC6im2U1IR36i6sv54D78AQH2ifK+QE1ph+MeIaSPMenbmtY3zVz/0sBOD2VxHIpeMZgX/YagILLQEfpNHJiybuRVS1ZtUWBNFji/6PBfQ16xtmiU17eppCuF9LJC0Hmf/wMw+4ZWVQiXBpV9bh4zP1EaVA1pYqv+kEbJhhoyhe5EIxrq8wLLgkBhWfKSJs+BfUVBZGHIwpQyhmxuSFFDyhhSxtAbKLlu2MKsEMD1dSQNvLNi1mJIUkZyqFl9nQz7xNyAZCP/2YwlNkuDwljir/hXGVLfpubdLvsZI1rGLmH/GQPa2pcY8OhQkdxRHhoonXLZ3FszOkt5sOhDES8IIxOCwrLBvU2Eh1DYnIMIwiYyTKhiB1m8tJHOacdAOnIQl8M6ElFhOvDLEJRkIRP64idtyU1IN5CpIyxiyUAQQUjEI8Qm0UHCNJEJjfjomA+rW8iwoKI7yIAJ8ki0OTPq0A7qMDhBOkY6b4ttRCxkEWTzaMYGD3LL4XOHTgmyNGTxphDOEMoyjKGFg3SuTU6kQAg9NI9TVlh5SsN5AY8wKIvmi2zFiONZoA6zeE06iMcXJ2tGp36aqWMQggVpuezJBWplVXx0FPojGsLm4Yz7A0KXfshDWfR/HkcZUr5A5LlJ4s+nbJye0SyDVin61b/0X/oZvfZAOlUTFEOL1fqILsYhC5gf/QTOwrvgHSK1eAsOVmu3YZlylHEcJ8HZTQoehK5/pknM1/UBNyGsS5ZtWpYJK/CNvGJgezAs/TicicY+d31TH2iOrhFDNx3LsR0w+k1+iVgD09GXPyQfml4WqvnXNFW2nCQ8rnLr88qP6UkcLk/NYxZlp/48WyRiJwZzSLhST6NJSIVtBb3CnmZ8MYqvz6RRddnX+5s51DQ5gdHkNA7jBEFkEhM2NpO8HMlSyPCZFVKakNGEhKZQYkFxHQ+JkBDlSJZCCmCXU8s11ZWaWFPDsFTwCXRedjLhM3yDtIhY9lJWvsfaH7//8Tu4KRtf5ArnzV4vZiPwusKPQeAZk7u6fAcrw+KSPoUBc7HVCeC7J7AyMlkbueSVa/54lM4T6gfplNLsdg/lK2jhobojZwaNzk9pGJ6VRTntKkk8lIKl7gGRxSxSBs3bOFvlcCFnadvkyFLO2ianF3LYwNsEjUJwuHVgc9mhoojbBa2SoF0RfBdfKbsoAxJlGBpyuoojhKZn4yQOQyF2WToei2GEFRK5z8kd3L+JF5zCwBU8uA9ahP5JaRvBTz8XDp8viVB/Ibs9WS6M/OxPpbOlxicwWkqTt7DnD1cuSL1fgHZ0tQXoKc+i4rQfhvHVGVAy80M3YFmcrF56D0vrezYvwod+XMDVd1CwhC4JyF9k8Wk8m4c0oyV/X4UDHNYT94Movy985cOaovW1/rh/gC0b46Fu9c/7+DG59RyGkjw25DXLNPMLRn7Bggu8buV1Ezro+33tsa4O8PKg2r+eN9NvuWauj2mpngx1QNSBlh/IeK/E99EFTQAwuc5EQPWLeJHKha9ktkVK3/rZ9GkUvKMT8L63Pt89ZcAmUnRJUgFAN4OG8rxiaM77/wZ2kmcDOkmoIrVQ3BtL5hVXtfKqVzktuvKSePZjdPkeFpW1qR4dKn2O0nHC5nztQiPYzl2UvCNgqQ+bwaDcDpRPQQsZWxnLOG8KP5pyF4Q2fiZ28+jVn/9NPsF+CpYrvp5fg0FTnkZQNPwUWArOHvf+8XERZ/86y+Lzc3koxoH4ncGdMsrEKgc7haxXailcFCIDxaNfIc6Xe3wpUUIEBDaseRAo86nPb9Ora6i2soIuZYu1FEgCwrFscDH0qzgowwDrhlTjVgucrFngZjaKw3omOHkgE9yHWqeraj1j42lG66l1usdqPVtV62kWzw4O31MWwu4smvlpSuFmCS3qKfpsjxV9qq8o+gI2+otZzcjU21QL7j3YNQ1WmfaOEFzXtWb47bmeKzOPFjOasPEyyOTkofVC9TrAtpMT2xadlotXHZVwTZXwRpVgEVtcs5D5yU0TTE/JCqYQlJPDmrQKTdvFld87w96QnS/3f3Cr8Ip3ZasEy4GR52Hq0VbFGnUp6q9nC3eVwmffYhR+V88a7v4Q9tbgflYJbkMN9fVHtluN7JroterLdyilliDgZVTVYx1gdyt7N5j7/cHire2Mok/+NERqa1QPIe/h9/QqL7Yue697ek+h6eroED3T0ffIXMkzwo/pklpQexWoycCybaPUleUS0jhw7w/555WAlPm8epg/3+OofK5w9DiOeKBxQ9fA7PndmDltAnYPofr86wzVrbCd+OEFjaZ//m9Kq/Sqt7t++hGbiQ/ZYKdD5zKrPadU5nmz/EMANIfuxGcI5aR1Te1fxLSqN2573/Dwev8Mzl8N15ZvhL4A3KTq418p1vVocPvtsL1ujdf+67+yNao7UFvtQO1aO9DNBvsS28/ttz+dB9NTYLo234DasAG1+O6l3o5zN2jvf7uilPHsZruwdvXYzjdO113UdRTfOLX4ZrPB2uebzoPpKTBdh/ON04xvdoP2/vlGKeM5zfimXT22882w6y7qDhXfDGvxzWaDtc83+w8m7+BhGUfB6Q454wybMc5u4N4/4yhlvGEzxmlXj+2Mg/Hee+lDUw5WiTZujDqks8Vm7bPO34B6BaCAFKcd+N2Id3bE9wEywUohTyjUgHpaVuUO7tG67qoumEBxj1aPezbbbA+4p/OAegWggJTgHq0h9+yG7wNwj1Zwj9aQe9pV5Q7uqSTWu+aqLiYF99QC1N1isz3gns4D6hWAAlKCe0hD7tkN3wfgHlJwD2nIPe2qsjI58c2xYmpv7vpE/m6XFB+53+PzqBt1yr+xkKJrORC6yctPpc+chXriW1KirV4+u/ZVh/rh/OaWR6c6/Lnnm78/Bl5ZvCve0TWud3HxKCKu9yziFpvtweLdeUC9AlBASizeesPFezd8H3i3bXQdXxdMoALWqBewm222BwHbeUC9AlBASgSs0TBgd8P3gQPW7Dq+Ln/nVB6wZr2A3WyzPQjYzgPqFYACUiJgzYYBuxu+DxywVtfxdfmLZvKAteoF7Gab7UHAdh5QrwAUkBIBazUM2N3wfeCA7fzjry4uHmbG9Z5m3mKzPQjYzgPqFYACUiJgGz7SvCO+OwbsOJ7N/ChAkXiJ3hn9uKD8taS8tXxtm68d997T6+wDf83OB9JHDP0TkV/66NsDbWDz6gGCWXz3C8wJH/cYFESY2tf5u/ZyRRZZuS8vDif5TPLxK2YKWbpMHy/bVBxL6NTge11EMz4/jbx8tVg2ZeOLCDxBvJ6p8Cp+8IIFAY0Kd6yXKT7AnwWMy6JPNByJL4d9YH0kMLKXGJW+NlYXH9kkYP4k8WezBiCtNbxnpOqSQAtI3bHmdT5p4BZJoHo5oH1OAXUeTK9IAIn8T8P0zz5nfzqfK3CL3E+91M8+Z346D6ZX5H1E2qdh1mefkz6dTxG4RcqnXsZnnxM+nQfTK9I9ItvTMNnTbq6n+uyS2hx4RrMnl9rdF1T1UOTpmc30aJc3q3oo5/KsZnrsm18Vzwl4uOHrblp+QuAWVYoYwQ2DpOXPTm9RpQgT3DBOWv5U6RZVikjBDUOl5Xz7LaoU7yTADV9K0G4m8rD85mZeV//d0pP/A1BLBwhm/xw2JgwAAB5qAABQSwECFAAUAAgICADTWXRCNdb7SLYCAADKCwAAEgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfbWFjcm8ueG1sUEsBAhQAFAAICAgA01l0QtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAA9gIAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADTWXRCZv8cNiYMAAAeagAADAAAAAAAAAAAAAAAAABTAwAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAvgAAALMPAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 +
 +
[[Kategorie:Stoffmenge]]
 +
[[Kategorie:Stöchiometrie]]
 +
[[Kategorie:Avogadro]]
 +
[[Kategorie:GeoGebra-Zeichnung]]

Aktuelle Version vom 13. Mai 2015, 20:34 Uhr

Wiederholung: Stöchiometrische Berechnungen bei der Reaktion von Feststoffen

Stoffmenge

Da die Atome so leicht sind, ist ihr Masse so gering, dass eine Rechnerei mit diesen Werten recht umständlich ist. Man kam deshalb auf die Idee, statt einzelner Atome immer gleich eine so große Anzahl an Atomen zu betrachten, dass man Massen im Gramm-Bereich hat.

Um nicht neue Massen-Werte zu bekommen, nutze man die Umrechnungszahl zwischen g und u und legte fest.

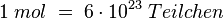
1 \;mol\;= \;6 \cdot 10^{23} \;Teilchen


Dabei ist die Zahl gerundet. Mit ein paar mehr Nachkommastellen hat man 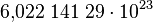6{,}022\;141\;29\cdot 10^{23} Der Begriff "Mol" wurde 1893 von Wilhelm Ostwald geprägt und ist vermutlich von "Molekül" abgeleitet. Die Angaben in "mol" Bezeichnet man Stoffmenge und man verwendet dafür den Buchstaben "n".

  • 1 mol Sauerstoff-Atome sind also etwa 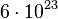6 \cdot 10^{23} Sauerstoff-Atome
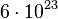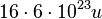  • Da 1 einzelnes Sauerstoff-Atom 16 u wiegt, wiegen dann 6 \cdot 10^{23} Sauerstoff-Atome 16 \cdot 6 \cdot 10^{23} u.
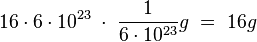
  • Wenn man u umrechnet hat man 16 \cdot 6 \cdot 10^{23}\;\cdot \;\frac{1}{6 \cdot 10^{23}}g\;=\;16 g
  • 1 mol Sauerstoff-Atome wiegen also gerade 16 g!

Für die Masse von einem Mol eines Stoffes führte man einen Namen ein:

Die Masse von einem Mol eines Stoffes entspricht der Masse von einem Teilchen in u, nur mit der Einheit g.

Man legt den Wert fest: Molmasse (oder Molare Masse) M mit der Einheit g/mol.


Nuvola apps korganizer.png   Aufgabe 1

Bestimme die Molare Masse der folgenden Stoffe:

  • Wasserstoff, Kohlendioxid, ..
Bei allen Rechnungen ist zu beachten, dass man die richtige Formel der Stoffe nimmt. Bei Gasen, die mehratomige Moleküle besitzen, muss man dies beachten.
  • Wasserstoff M(H2)= 2 g/mol
  • Kohlendioxid M(CO2)= (12 + 16 * 2) g/mol = 48 g/mol


Satz von Avogadro

Avogadro Amedeo.jpg

Der Italienier Amedeo Avogardo war Professor für mathematische Phsik und untersuchte im 19. Jahrhundert Gase und stieß dabei auf eine Besonderheit bei der Anzahl der Gasteilchen pro Volumeneinheit.

Da wir die Experimente praktisch nicht nachvollziehen können, gehen wir eher theoretisch an und schauen uns bekannte Messwerte zu Gasen an, nämlich deren Dichte.

Da wir ja inzwischen wissen, wie die Masse von einem Atom ist können wir über die Dichte die Anzahl der Atome in einer Gasportion berechnen. Genauer: Es soll bestimmt werden, wieviele Teilchen in in einem Liter eines Gases enthalten ist. Dies soll hier am Beispiel von Helium gezeigt werden. Dabei gehen wie folgendermaßen vor:

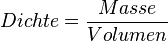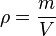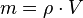  • 1. Schritt: Berechne die Masse von 1 Liter des Gases. Dazu nutzen wir die Formel der Dichte Dichte = \frac{Masse}{Volumen} bzw. mit Symbolen \rho = \frac{m}{V}, die wir nach der Masse m umformen m = \rho \cdot V.
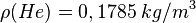\rho(He)= 0,1785\;kg/m^3,

dann ist m(1 l\;Helium)=\rho(He) \cdot V(He)\;=\;0,1785\;kg/m^3 \cdot 1\;l.
Die Einheit kg/m3 entspricht g/l (man kürzt mit 1000! 1 kg = 1000 g und 1m³ = 1000 dm³ = 1000 l)
und deshalb kann man rechnen: m(1 l\;Helium)=\;0,1785\;kg/m^3 \cdot 1\;l=0,1785\;g

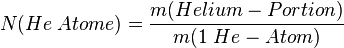
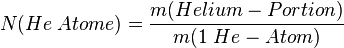  • 2. Schritt: Dann berechnet man, wieviele Teilchen enthalten sind, denn man weiß ja was ein Teilchen wiegt. N(He\;Atome) = \frac{m(Helium-Portion)}{m(1\; He-Atom)}
N(He\;Atome) = \frac{m(Helium-Portion)}{m(1\; He-Atom)}

Ein Helium-Atom wiegt ja 4 u. Die Einheit u kann man in g umrechnen mit dem Faktor 6 \cdot 10 ^{23}. So hat man dann:
N(He\;Atome) = \frac{m(Helium-Portion)}{m(1\; He-Atom)}=\frac{0,1785 g}{4 u}=\frac{0,1785 \;g}{4\;\frac{1}{6 \cdot 10 ^{23}}\;g}=2,6775 \cdot 10^{22}



Um die gleiche Rechnung für verschiedene Gase etwas schneller durchführen zu können, habe ich ein GeoGebra-Applet vorbereitet. Bei der Eingabe der Datei bitte folgendes beachten:

  • Kommazahlen werden in GeoGebra mit dem Punkt "." statt dem "," eingegeben. Sonst wird es als Text angesehen.
  • Text sollte zur Sicherheit immer in Anführungsstrichen geschrieben werden, damit mit zum Beispiel H2 als Name für die Zelle "H2" angesehen wird.

Die Daten zu den Dichten von Elementen erhält man aus der Liste im Buch. Eine größere Liste auch mit Dichten von vielen Verbindungen, findet man [hier].

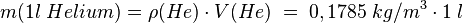Von „http://chemie-digital.zum.de/index.php?title=Frau_Lachner/Berechnungen_von_Massen_bei_Reaktionen&oldid=3672“