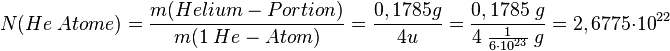Berechnungen von Massen bei Reaktionen: Unterschied zwischen den Versionen

Aus Chemie digital
Wechseln zu: Navigation, Suche
(→‎Satz von Avogadro)
(→‎Satz von Avogadro)
Zeile 18: Zeile 18:
 
<math>N(He\;Atome) = \frac{m(Helium-Portion)}{m(1\; He-Atom)}=\frac{0,1785 g}{4 u}=\frac{0,1785 \;g}{4\;\frac{1}{6 \cdot 10 ^{23}}\;g}=2,6775 \cdot 10^{22}</math>
 
<math>N(He\;Atome) = \frac{m(Helium-Portion)}{m(1\; He-Atom)}=\frac{0,1785 g}{4 u}=\frac{0,1785 \;g}{4\;\frac{1}{6 \cdot 10 ^{23}}\;g}=2,6775 \cdot 10^{22}</math>
 
}}
 
}}
−
* <u>3. Schritt:</u>
+
 
 +
 
 +
 
 +
 
 +
Um die gleiche Rechnung für verschiedene Gase etwas schneller durchführen zu können, habe ich ein GeoGebra-Applet vorbereitet.
 +
<ggb_applet width="1100" height="466"  version="4.2" ggbBase64="UEsDBBQACAgIALBZdEIAAAAAAAAAAAAAAAASAAAAZ2VvZ2VicmFfbWFjcm8ueG1s7VbNTtwwED7DU1g+UbXkZxeqCm1AArUCqUAlOFS9TZwhcXHsKPayuzxYX6AvVv8kS3YRLUUcSsUevBN7/r5vZpxMDua1IDfYaq5kRtMooQQlUwWXZUan5mr7Az3Y35yUqErMWyBXqq3BZHQnGtE7O/sUjXadMZlrvifVGdSoG2B4wSqs4bNiYLxmZUyzF8ez2SzqfUaqLeOyNNFcF5TYfKTOaCfsWXcrRrOxVx8lSRp/Pf0c3G9zqQ1IhpTYXGtgrSKsLlwSGf3I5S2KHMQ1SkqMUuKh/WMUjYvMmZKfuEAn60rNTuSlPT2ENqOmndogTDWLI2gcIt3t9XFPZDM1BJKMHiusrC6kGf0GlbDSKKOHPlz184c9inub86npjcK5P7JJaOuauSjEcBPygampVOukAozbsZoosEZpiFk0dkdOa2w5o0RAjmI15P7mxuQGxBSJXTOaRGMXamPiUBKVf0dmS3sFQuPS3KPzSvb8SAnVEhveVrr0a+5XEE0Fzl8aVAUssO1i9DvW26kqusidHkhe+8Yg2mDjtoluEAsvBTjWe2Pd+X4MmTly4g7zH9GHKqzhTl2r/ufAfc+t4T6Ds5cPm6m6BlkQ6af4ixKLUkmPlC9nbyt5R3zlyVsy6P83YRzvTrfXT+2IbjnmHlQYryms+Q/E3ZtnHxaC/zx4sZWCnYwWAV4H6l5Vmw7e6jB7tIJLvDALgcRUnF1L1PYuGg1odMIxLwqUS/5X6h7uss7xkurVuqe7Y1/53fTJpU9+37caS/e0TATocyea/E2iG7a/VFtoMnem75PhL92hZBE8ktuh5ydUwvaIcE1+Io19iaK/5XXIY4DwGrG5tMbn8rIFqd3LN+j0U/p4XvN/h1d3DTki/f/t4Fp6EUSyVyKfh8jilcjHEhkPPwbds/9udEL/Eb3/C1BLBwg11vtItgIAAMoLAABQSwMEFAAICAgAsFl0QgAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK4FAFBLBwjWN725GQAAABcAAABQSwMEFAAICAgAsFl0QgAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWztXety2zYW/p0+BUY/dtquLBPgVVk7ndghk87kNnG2s9NMf1AiLKGmSIWkfMn0cfYJ+mMfoH2xPQAIihItmYzsUCnrJAZBHlzO+c75AB5RzNEP17MQXdIkZXF03MMDrYdoNI4DFk2Oe4vs/MDp/fDkm6MJjSd0lPjoPE5mfnbcMwakt2wHtQExeWMWHPccR6PBcBgc2DrVDgyDBgeOcR4cGL5pG2N6ToeU9hC6TtnjKH7tz2g698f0bDylM/9lPPYz0ec0y+aPDw+vrq4GavRBnEwOJ5PR4DoNeghmHqXHvfzgMXS30uhKF+JE0/Dhf169lN0fsCjN/GgM43OtFuzJN4+OrlgUxFfoigXZFGyAsdlDU8omU9DT0kCpQy41B2XndJyxS5pC21JVKJ3N5j0h5kf8+iN5hMJCnx4K2CULaHLc0wYmNuyhQzSL2I5GrGEPxQmjUZbL4nzMQ9Xb0SWjV7JbfiRGNLShDRiwlI1Cetw798MU1GLReQImhQklC6im2U1IR36i6sv54D78AQH2ifK+QE1ph+MeIaSPMenbmtY3zVz/0sBOD2VxHIpeMZgX/YagILLQEfpNHJiybuRVS1ZtUWBNFji/6PBfQ16xtmiU17eppCuF9LJC0Hmf/wMw+4ZWVQiXBpV9bh4zP1EaVA1pYqv+kEbJhhoyhe5EIxrq8wLLgkBhWfKSJs+BfUVBZGHIwpQyhmxuSFFDyhhSxtAbKLlu2MKsEMD1dSSbR1x3zopVixFJGcihZvV1MuwTcwOQjdxnM5TYLA0KY4m/4l9lSJ3s5LGfMaJl7BL1nzGgrX2JAY8OFccd5ZGB0imXzV0no7OUx4o+FOGCMDIhJiwbvNtEeAiFzSmIIGwiw4QqdpDFSxvpnHUMpCMHcTmsIxEUpgO/DMFIFjKhL37SltSEdAOZOsIilAwEAYREOEJoEh0kTBOZ0IiPjvmwuoUMCyq6gwyYIA9EmxOjDu2gDoMTpGOk87bYRsRCFkE2D2Zs8Bi3HD536JQgS0MWbwrRDJEsoxhaOEjn2uQ8CnzQQ/M4ZYWVpzScF/AIg7JovshWjDieBeowi9ekg3h8cbJmdOqnmToGIViPlqueXJ9WFsVHR6E/oiHsHc64PyB06Yc8lEX/53GUIeULRJ6bJP58ysbpGc0yaJWiX/1L/6Wf0WsPpFM1QTG0WKyP6GIcsoD50U/gLLwL3iFSa7egYLV0G5YpRxnHcRKc3aTgQej6Z5rEfFkfcBPCsmTZpmWZsADfyCsGtgfD0o/DmWjsc9c39YHm6BoxdNOxHNsBo9/kl4g1MB19+UPyoelloZp/TVNly0nC4yq3Pq/8mJ7E4fLUPGZRdurPs0UiNmIwh4Qr9TSahFTYVrArbGnGF6P4+kwaVZd9vb+ZQ02TExhNTuMwThBEJjFhXzPJy5EshQyfWSGlCRlNSGgKJRYU1/GQCAlRjmQppAB2ObVcU12piTU1DEsFn0DnZScTPsP3R4uIZS9l5Xus/fH7H7+Dm7LxRa5w3uz1YjYCryv8GASeMbmpyzewMiwu6VMYMBdbnQC+ewIrI5O1kUteueaPR+k8oX6QTinNbvdQvoAWHqo7cmbQ6PyUhuFZWZTTrpLEQylY6h4QWcwiZdC8jbNVDhdylrZNjizlrG1yeiGHDbxN0CgEh1sHNpcdKoq4XdAqCdoVwXfxlbKLMiBRhqEhp6s4Qmh6Nk7iMBRil6XjsRhGWCGR25zcwf2beMEpDFzBg9ugReiflLYR/PRz4fD5kgj1F7Lbk+XCyM/+VDpbanwCo6U0eQtb/nDlgtT7BWhHV1uAnvIsKk77YRhfnQElMz90A5bFyeql97C0vmfzInzoxwVcfQcFS+iSgPxFFp/Gs3lIM1ry91U4wGE9cTuI8tvCVz6sKVpf64/7B9iyMR7qVv+8jx+TW89hKMljQ16zTDO/YOQXLLjA61ZeN6GDvt/XHuvqAC8Pqv3reTP9lmvm+piW6slQB0QdaPmBjPdKfB9d0AQAk+tMBFS/iBepXPhKZluk9K2fTZ9GwTs6Ae976/PdUwZsIkWXJBUAdDNoKM8rhua8/29gJ3k2oJOEKlILxa2xZF5xVSuvepXToisviWc/RpfvYVFZm+rRodLnKB0nbM7XLjSC7dxFyTsClvqwGQzK7UD5FLSQsZWxjPOm8KMpd0Fo42diN49e/fnf5BPsp2C54uv5NRg05VkERcNPgaXg7HHvHx8Xcfavsyw+P5eHYhyI3xncKKNMrHKwU8h6pZbCRSEyUDz6FeJ8uceXEiVEQGDDmgeBMp/6/C69uoZqKyvoUrZYS4EkIBzLBhdDv4qDMgywbkg1brXAyZoFbmajOKxngpMHMsF9qHW6qtYzNp5mtJ5ap3us1rNVtZ5m8ezg8D1lIezOopmfphRultCinqLP9ljRp/qKoi9go7+Y1YxMvU214N6DXdNglWnvCMF1XWuG357ruTLzaDGjCRsvg0xOHlovVK8DbDs5sW3Rabl41VEJ11QJb1QJFrHFNQuZn9w0wfSUrGAKQTk5rEmr0LRdXPm9M+wN2fly/we3Cq94V7ZKsBwYeR6mHm1VrFGXov56tnBXKXz2LUbhd/Ws4e4PYW8N7meV4DbUUF9/ZLvVyK6JXqu+fIdSagkCXkZVPdYBdreyd4O53x8s3trOKPrkT0Oktkb1EPIefk+v8mLrsve6p/cUmq6ODtEzHX2PzJU8I/yYLqkFtVeBmgws2zZKXVkuIY0D9/6Qf14JSJnPq4f58z2OyucKR4/jiAcaN3QNzJ7fjZnTJmD3EKrPv85Q3QrbiR9e0Gj65/+mtEqvervrpx+xmfiQDXY6dC6z2nNKZZ43yz8EQHPoTnyGUE5a19T+RUyreuO29w0Pr/fP4PzVcG35RugLwE2qPv6VYl2PBrffDtvr1njtv/4rW6O6A7XVDtSutQPdbLAvsf3cfvvTeTA9BaZr8w2oDRtQi+9e6u04d4P2/rcrShnPbrYLa1eP7XzjdN1FXUfxjVOLbzYbrH2+6TyYngLTdTjfOM34Zjdo759vlDKe04xv2tVjO98Mu+6i7lDxzbAW32w2WPt8s/9g8g4elnEUnO6QM86wGePsBu79M45Sxhs2Y5x29djOOBjvvZc+NOVglWjjxqhDOlts1j7r/A2oVwAKSHHagd+NeGdHfB8gE6wU8oRCDainZVXu4B6t667qggkU92j1uGezzfaAezoPqFcACkgJ7tEacs9u+D4A92gF92gNuaddVe7gnkpivWuu6mJScE8tQN0tNtsD7uk8oF4BKCAluIc05J7d8H0A7iEF95CG3NOuKiuTE98cK6b25q5P5O92SfGR+z0+j7pRp/wbCym6lgOhm7z8VPrMWagnviUl2urls2tfdagfzm9ueXSqw597vvn7Y+CVxbviHV3jehcXjyLies8ibrHZHizenQfUKwAFpMTirTdcvHfD94F320bX8XXBBCpgjXoBu9lmexCwnQfUKwAFpETAGg0Ddjd8Hzhgza7j6/JXTuUBa9YL2M0224OA7TygXgEoICUC1mwYsLvh+8ABa3UdX5e/aCYPWKtewG622R4EbOcB9QpAASkRsFbDgN0N3wcO2M4//uri4mFmXO9p5i0224OA7TygXgEoICUCtuEjzTviu2PAjuPZzI8CFImX6J3RjwvK30rKW8vXtvnace89vc4+8NfsfCB9xNA/Efmlj7490AY2rx4gmMV3v8Cc8HGPQUGEqX2dv2svV2SRlfvy4nCSzyQfv2KmkKXL9PGyTcWxhE4NvtdFNOPz08jLV4tlUza+iMATxOuZCq/iBy9YENCocMd6meID/FnAuCz6RMOR+HLYB9ZHAiN7iVHpa2N18ZFNAuZPEn82awDSWsN7RqouCbSA1B1rXueTBm6RBKqXA9rnFFDnwfSKBJDI/zRM/+xz9qfzuQK3yP3US/3sc+an82B6Rd5HpH0aZn32OenT+RSBW6R86mV89jnh03kwvSLdI7I9DZM97eZ6qs8uqc2BZzR7cqndfUFVD0WentlMj3Z5s6qHci7PaqbHvvlV8ZyAhxu+7qblJwRuUaWIEdwwSFr+7PQWVYowwQ3jpOVPlW5RpYgU3DBUWs6336JK8U4C3PClBO1mIg/Lb27mdfW/LT35P1BLBwj2krrcJgwAAB1qAABQSwECFAAUAAgICACwWXRCNdb7SLYCAADKCwAAEgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfbWFjcm8ueG1sUEsBAhQAFAAICAgAsFl0QtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAA9gIAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICACwWXRC9pK63CYMAAAdagAADAAAAAAAAAAAAAAAAABTAwAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAvgAAALMPAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Version vom 20. März 2013, 11:13 Uhr

Wiederholung: Stöchiometrische Berechnungen bei der Reaktion von Feststoffen

Satz von Avogadro

Avogadro Amedeo.jpg

Der Italienier Amedeo Avogardo war Professor für mathematische Phsik und untersuchte im 19. Jahrhundert Gase und stieß dabei auf eine Besonderheit bei der Anzahl der Gasteilchen pro Volumeneinheit.

Da wir die Experimente praktisch nicht nachvollziehen können, gehen wir eher theoretisch an und schauen uns bekannte Messwerte zu Gasen an, nämlich deren Dichte.

Da wir ja inzwischen wissen, wie die Masse von einem Atom ist können wir über die Dichte die Anzahl der Atome in einer Gasportion berechnen. Genauer: Es soll bestimmt werden, wieviele Teilchen in in einem Liter eines Gases enthalten ist. Dies soll hier am Beispiel von Helium gezeigt werden. Dabei gehen wie folgendermaßen vor:

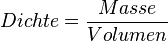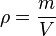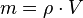  • 1. Schritt: Berechne die Masse von 1 Liter des Gases. Dazu nutzen wir die Formel der Dichte Dichte = \frac{Masse}{Volumen} bzw. mit Symbolen \rho = \frac{m}{V}, die wir nach der Masse m umformen m = \rho \cdot V.
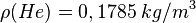\rho(He)= 0,1785\;kg/m^3,

dann ist m(1 l\;Helium)=\rho(He) \cdot V(He)\;=\;0,1785\;kg/m^3 \cdot 1\;l.
Die Einheit kg/m3 entspricht g/l (man kürzt mit 1000! 1 kg = 1000 g und 1m³ = 1000 dm³ = 1000 l)
und deshalb kann man rechnen: m(1 l\;Helium)=\;0,1785\;kg/m^3 \cdot 1\;l=0,1785\;g

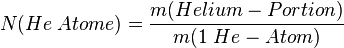
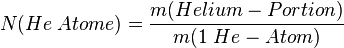  • 2. Schritt: Dann berechnet man, wieviele Teilchen enthalten sind, denn man weiß ja was ein Teilchen wiegt. N(He\;Atome) = \frac{m(Helium-Portion)}{m(1\; He-Atom)}
N(He\;Atome) = \frac{m(Helium-Portion)}{m(1\; He-Atom)}

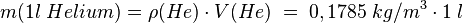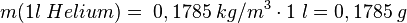
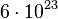Ein Helium-Atom wiegt ja 4 u. Die Einheit u kann man in g umrechnen mit dem Faktor 6 \cdot 10 ^{23}. So hat man dann:
N(He\;Atome) = \frac{m(Helium-Portion)}{m(1\; He-Atom)}=\frac{0,1785 g}{4 u}=\frac{0,1785 \;g}{4\;\frac{1}{6 \cdot 10 ^{23}}\;g}=2,6775 \cdot 10^{22}



Um die gleiche Rechnung für verschiedene Gase etwas schneller durchführen zu können, habe ich ein GeoGebra-Applet vorbereitet.

Von „http://chemie-digital.zum.de/index.php?title=Frau_Lachner/Berechnungen_von_Massen_bei_Reaktionen&oldid=1790“