Benzol und die Aromaten: Unterschied zwischen den Versionen

Version vom 30. März 2018, 09:12 Uhr (Quelltext anzeigen) B.Lachner (Diskussion | Beiträge) (→‎Das Orbitalmodell als Erklärung für die merkwürdige Benzol-Struktur) ← Zum vorherigen Versionsunterschied		Version vom 30. März 2018, 10:57 Uhr (Quelltext anzeigen) B.Lachner (Diskussion | Beiträge) (→‎Das Orbitalmodell als Erklärung für die merkwürdige Benzol-Struktur) Zum nächsten Versionsunterschied →
Zeile 57:		Zeile 57:
	{{Kurzregel|Aus diesen Videos lernt man: ''Kleine Teilchen wie Elektronen und Photonen können sich wie eine Welle oder wie ein Teilchen verhalten.'' Man nennt diese Eigenschaft "Welle-Teilchen-Dualismus".}}		{{Kurzregel|Aus diesen Videos lernt man: ''Kleine Teilchen wie Elektronen und Photonen können sich wie eine Welle oder wie ein Teilchen verhalten.'' Man nennt diese Eigenschaft "Welle-Teilchen-Dualismus".}}
−	[[Datei:Broglie Big.jpg|right|200px]]De Broglie gilt als einer der bedeutendsten Physiker des 20. Jahrhunderts, der für seine Entdeckung der Wellennatur des Elektrons in seiner Dissertation 1929 den Nobelpreis für Physik erhielt.	+	[[Datei:Broglie Big.jpg|right|100px]]De Broglie gilt als einer der bedeutendsten Physiker des 20. Jahrhunderts, der für seine Entdeckung der Wellennatur des Elektrons in seiner Dissertation 1929 den Nobelpreis für Physik erhielt.
		+
		+
	Mit der Möglichkeit Elektronen als Wellen anzusehen, ergaben sich neue Möglichkeiten die Bewegung bzw. die Position der Elektronen in der Atomhülle neu zu beschreiben.		Mit der Möglichkeit Elektronen als Wellen anzusehen, ergaben sich neue Möglichkeiten die Bewegung bzw. die Position der Elektronen in der Atomhülle neu zu beschreiben.
−	Elektronen als stehende Wellen in Elektronenschalen ermöglichen eine Erklärung für die Strahlungsfreiheit. Indem man die Wellenlängen der Elektronen in Abhängigkeit vom Umfang der  Elektronbahn so festlegte, dass sich stehende Welle ausbilden können. Da diese ihre Energie speichert, bleibt dadurch auch das Elektron strahlungsfrei.	+	Elektronen als '''stehende Wellen''' in Elektronenschalen ermöglichen eine Erklärung für die Strahlungsfreiheit. Indem man die Wellenlängen der Elektronen in Abhängigkeit vom Umfang der  Elektronbahn so festlegte, dass sich stehende Welle ausbilden können. Da diese ihre Energie speichert, bleibt dadurch auch das Elektron strahlungsfrei.
		+
		+	Die folgende Animation zeigt eindimensionale stehende Wellen mit verschiedenen Frequenzen und Wellenlängen:
	[[File:Vibration corde trois modes petit.gif]]		[[File:Vibration corde trois modes petit.gif]]
		+
		+	Das Prinzip der stehenden Welle kann auf die Schalen der Atome übertragen werden. Die folgende Animation soll nur das Prinzip zeigen, dass bei größeren Schalen mehr Möglichkeiten zu unterschiedlichen Schwingungen bestehen.
		+
		+	<iframe scrolling="no" title="Elektronen als stehende Wellen auf den Schalen" src="https://www.geogebra.org/material/iframe/id/AZ38VxSp/width/950/height/730/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="950px" height="730px" style="border:0px;"> </iframe>
		+
		+	Die folgenden Videos zeigen weitere Beispiele für Schwingungen und stehende Wellen in verschiedenen Dimensionen.
		+	* [http://www.quantenspiegelungen.de/subdimension-linie-u2/kugelschwingungen/chladni-figuren/ Chladnische-Klang-Figuren] verdeutlichen zwei-dimensionale stehende Wellen, ebenso wie das [http://www.quantenspiegelungen.de/subdimension-linie-u2/kugelschwingungen/schwingende-tasse/ Schwingungsverhalten einer Kaffee-Tasse].
		+	* Bei [http://www.quantenspiegelungen.de/subdimension-linie-u2/kugelschwingungen/schwingende-seifenblase/ schwingenden Seifenblasen] kann man stehende Wellen bei drei-dimensionalen Körpern erzeugen. Verallgemeinert kann dies in [http://www.quantenspiegelungen.de/subdimension-linie-u2/kugelschwingungen/kugelflaechenfunktion/ Schwingungen bei Kugeloberflächen], die man aber nicht so einfach in einem realen Experiment darstellen kann. Dazu kommen weitere Schwingunsarten, die sich bei der Seifenblase nicht erzeugen lassen.
		+	* Das folgende Video ist nicht so einfach zu verstehen, aber es beschreibt den Übergang von den stehenden Wellen aus den verschiedenen Beispielen hin zu den Zuständen, die für das eine [http://www.quantenspiegelungen.de/subdimension-linie-u2/atommodelle/zustaende-operationen-beim-h-atom/ Elektron bei einem Wasserstoff-Atom] möglich sind. '''ACHTUNG - nur für Physik-Leistungs-Kursler zu empfehlen!'''
		+
		+	[[File:Erwin Schrodinger2.jpg|right|100px]]Die berühmte '''Schrödinger-Gleichung''' kann man vereinfacht so verstehen, dass sie beschreibt, unter welchen Bedingungen Elektronen-Wellen einen stabilen Zustand haben, also eine stehende Welle sind. Es gibt aber nicht nur eine Lösung für diese Gleichung, denn die "Lösung" hängt von Parametern ab, wie etwa die Schalennummer ''(meist mit '''n''' bezeichnet)'', die Anzahl der Knotenlinien ''(mit '''l''' bezeichnet, mit ganzzahligen Werten von 0 bis n-1)'', wie sie auch in den gezeigten Animationen vorkommen und deren räumliche Ausrichtungen (mit ganzahligen Werten von -l bis +l). Dazu kommen noch der sogenannte Spin für die Drehrichtung der "Welle".
		+
		+	Aus diesen Möglichkeiten ergeben sich die sogenannten Orbitale als die Bereiche, in denen die Wahrscheinlichkeit am größten ist, dass sich das betreffende Elektron dort aufhält. Das Video [http://www.quantenspiegelungen.de/subdimension-linie-u2/atommodelle/atomorbitale/ Atomorbitale] zeigt, wie man von den Stehenden Wellen zu den Atomorbitalen kommt.
		+
		+
		+	Man kann daher die verschiedenen Elektronen in Atomen mit Hilfe von vier verschiedenen Quantenzahlen beschreiben:
		+	* Die '''Hauptquantenzahl n'''  entspricht der Schalennummer n = 1, 2 ,3, ...
		+	* Die '''Nebenquantenzahl l''' gibt die Form
		+
		+	http://www.quantenspiegelungen.de/subdimension-linie-u2/atommodelle/atomorbitale/
		+
		+

---

Version vom 30. März 2018, 10:57 Uhr

Inhaltsverzeichnis 1 Benzol und seine mysteriöse Struktur 1.1 Geschichte von Benzol 1.2 Strukturfindung von Benzol 2 Das Orbitalmodell als Erklärung für die merkwürdige Benzol-Struktur 2.1 Formen der Orbitale 2.2 Energiestufen der Orbitale 2.3 Hybridisierung 2.4 Orbital-Modell bei Mehrfachbindungen

Benzol und seine mysteriöse Struktur

Benzol (auf englisch Benzene) ist eine flüssige, organische Verbindung mit einem charakteristischen aromatischen Geruch. Dieser Geruch prägt eine Gruppe von Verbindungen, deren Struktur ähnlich wie die vom Benzol sind und daher den Namen Aromaten bekommen haben. Die Verbindung mit der Summenformel C₆H₆ ist ein Kohlenwasserstoff und der einfachste Vertreter dieser Gruppe. Benzol ist mischbar mit fast allen organischen Lösungsmitteln, jedoch kaum mit Wasser. Als Lösungsmittel war Benzol früher sehr gebräuchlich. Es hat seine Bedeutung verloren, da es krebserregend ist. Im Benzin kommt es noch vor.

Geschichte von Benzol

Der Name Benzol wurde im Jahr 1843 erstmals von Justus von Liebig verwendet. Liebig änderte damit die seit 1833 gebräuchliche Bezeichnung, nach der das Benzol als "Benzin" bezeichnet wurde. Im englisch- und französisch-sprachigen Raum wurde die alten Bezeichnung (franz: benzène, engl: benzene) weiterhin benutzt.

In der zweiten Hälfte des 17. Jahrhunderts wurde Benzol von Johann Rudolph Glauber bei der Destillation von Steinkohlenteer entdeckt. Die Zusammensetzung war für ihn jedoch unbekannt, daher nannte er es ein „subtiles und liebliches Oleum“, vermutlich wegen dem auffälligen Geruch.

Im Jahre 1825 wurde Benzol von dem englischen Physiker Michael Faraday im Leuchtgas entdeckt, als er dieses Öl aus flüssigen Rückständen isolierte, die sich beim Verbrennen von Walölen in den Londoner Straßenlaternen aus der Gasphase abschieden. Er schlug deshalb den Namen „Pheno“ (gr. phainein = leuchten) vor. Diese Vorsilbe findet sich in der Bezeichnung Phenol wieder, ein Stoff bei dem es sich um Benzol mit einer OH-Gruppe handel, also ein "Phen"-Alkohol.

Ein Jahr später erkannte man das dieses "Öl" ein reiner Kohlenwasserstoff ist.

Im Jahre 1834 stellte der deutsche Chemiker Eilhard Mitscherlich Benzol aus Benzoesäure und Calciumoxid, außerdem setzte er Benzol zu Nitrobenzol, Azobenzol und Benzolsulfonsäure um. Er benannte den Stoff wegen seiner Verwandtschaft zu Benzoesäure als „Benzin“. Außerdem erstellte er die richtige Summenformel C₆H₆.

1845 isolierte der englische Chemiker Charles Mansfield während seiner Arbeit unter Leitung von August Wilhelm von Hofmann Benzol ebenfalls aus Steinkohlenteer.

Strukturfindung von Benzol

Um die korrekte Strukturformel des Benzols herrschte lange ein Streit unter den Gelehrten. Es folgten viele Vorschläge, die in der Tabelle aufgeführt wurden.

Erst im Jahre 1861 formulierte der österreichische Chemiker Loschmidt, damals noch Schullehrer, einige mögliche Strukturformeln des Benzols, von denen man vermutet, dass sie die der deutsche Chemiker August Kekulé dann 1865 als Anregung für seine Kekulé-Strukturformel übernahm. Einer Legende nach kam Kekulé dieser Einfall im Traum. Er träumte von einer Schlange, die sich selbst in den Schwanz biss. Kekulé beschreibt dies in seiner Rede zum 25-jährigen Jubiläum des Benzolrings 1890.

Kekulés Struktur war die erste, die die Tatsache, das man beim Benzol festegestellt hat, dass alle Kohlenstoffatome gleichwertig sind, erklären konnte. Allerdings konnten damit noch nicht alle Besonderheiten des Benzols erklärt werden, wie beispielsweise seine ungewöhnlich niedrige Reaktivität. Merkwürdig war zum Beispiel, dass Benzol nicht Bromwasser reagiert, was bei Strukturformel mit drei Doppelbindungen eigentlich zu erwarten wäre. Der Beweis der Gleichwertigkeit der Wasserstoffe im Benzolmolekül konnte von 1869 bis 1874 erbracht werden.

Vorgeschlagene Strukturformeln
Von Adolf Karl Ludwig Claus (1867)	Von James Dewar (1867)	Prisman-Struktur von Albert Ladenburg (1869)	Von Henry Edward Armstrong (1887), [Adolf von Baeyer (1888)	Von Friedrich Karl Johannes Thiele (1899)	Von August Kekulé (1872)

Das Orbitalmodell als Erklärung für die merkwürdige Benzol-Struktur

Das wir die Elektronen, die ja für die Atom-Bindungen zuständig sind, neu betrachten müssen, wird in den folgenden Videos gezeigt. Es geht dabei um das sogenannte Doppelspalt-Experiment, das den Wissenschaftler Rätsel aufgab:

Videos zum Doppelspalt-Experiment:

• 01 Das Reich der Quanten und Elementarteilchen ... sehr ausführliches und gut erklärendes Video zum Doppelspaltxperiment bei Photonen.
  • Das Mysterium - Quantenbewusstsein ... als Comic dargestellt, kürzer aber nicht so genau.

Filme auf dem Rheinland-Pfälzischen Omega-Server (nur mit Account nutzbar)

• Elektronen als stehende Wellen
• Quantenmechanik und Orbitalmodelle

Aus diesen Videos lernt man: Kleine Teilchen wie Elektronen und Photonen können sich wie eine Welle oder wie ein Teilchen verhalten. Man nennt diese Eigenschaft "Welle-Teilchen-Dualismus".

De Broglie gilt als einer der bedeutendsten Physiker des 20. Jahrhunderts, der für seine Entdeckung der Wellennatur des Elektrons in seiner Dissertation 1929 den Nobelpreis für Physik erhielt.

Mit der Möglichkeit Elektronen als Wellen anzusehen, ergaben sich neue Möglichkeiten die Bewegung bzw. die Position der Elektronen in der Atomhülle neu zu beschreiben. Elektronen als stehende Wellen in Elektronenschalen ermöglichen eine Erklärung für die Strahlungsfreiheit. Indem man die Wellenlängen der Elektronen in Abhängigkeit vom Umfang der Elektronbahn so festlegte, dass sich stehende Welle ausbilden können. Da diese ihre Energie speichert, bleibt dadurch auch das Elektron strahlungsfrei.

Die folgende Animation zeigt eindimensionale stehende Wellen mit verschiedenen Frequenzen und Wellenlängen:

Das Prinzip der stehenden Welle kann auf die Schalen der Atome übertragen werden. Die folgende Animation soll nur das Prinzip zeigen, dass bei größeren Schalen mehr Möglichkeiten zu unterschiedlichen Schwingungen bestehen.

Die folgenden Videos zeigen weitere Beispiele für Schwingungen und stehende Wellen in verschiedenen Dimensionen.

• Chladnische-Klang-Figuren verdeutlichen zwei-dimensionale stehende Wellen, ebenso wie das Schwingungsverhalten einer Kaffee-Tasse.
• Bei schwingenden Seifenblasen kann man stehende Wellen bei drei-dimensionalen Körpern erzeugen. Verallgemeinert kann dies in Schwingungen bei Kugeloberflächen, die man aber nicht so einfach in einem realen Experiment darstellen kann. Dazu kommen weitere Schwingunsarten, die sich bei der Seifenblase nicht erzeugen lassen.
• Das folgende Video ist nicht so einfach zu verstehen, aber es beschreibt den Übergang von den stehenden Wellen aus den verschiedenen Beispielen hin zu den Zuständen, die für das eine Elektron bei einem Wasserstoff-Atom möglich sind. ACHTUNG - nur für Physik-Leistungs-Kursler zu empfehlen!

Die berühmte Schrödinger-Gleichung kann man vereinfacht so verstehen, dass sie beschreibt, unter welchen Bedingungen Elektronen-Wellen einen stabilen Zustand haben, also eine stehende Welle sind. Es gibt aber nicht nur eine Lösung für diese Gleichung, denn die "Lösung" hängt von Parametern ab, wie etwa die Schalennummer (meist mit n bezeichnet), die Anzahl der Knotenlinien (mit l bezeichnet, mit ganzzahligen Werten von 0 bis n-1), wie sie auch in den gezeigten Animationen vorkommen und deren räumliche Ausrichtungen (mit ganzahligen Werten von -l bis +l). Dazu kommen noch der sogenannte Spin für die Drehrichtung der "Welle".

Aus diesen Möglichkeiten ergeben sich die sogenannten Orbitale als die Bereiche, in denen die Wahrscheinlichkeit am größten ist, dass sich das betreffende Elektron dort aufhält. Das Video Atomorbitale zeigt, wie man von den Stehenden Wellen zu den Atomorbitalen kommt.

Man kann daher die verschiedenen Elektronen in Atomen mit Hilfe von vier verschiedenen Quantenzahlen beschreiben:

• Die Hauptquantenzahl n entspricht der Schalennummer n = 1, 2 ,3, ...
• Die Nebenquantenzahl l gibt die Form

http://www.quantenspiegelungen.de/subdimension-linie-u2/atommodelle/atomorbitale/

• http://www.quantenwelt.de/quantenmechanik/wellenfunktion/schrodinger.html
• Schrödinger-Gleichung

Formen der Orbitale

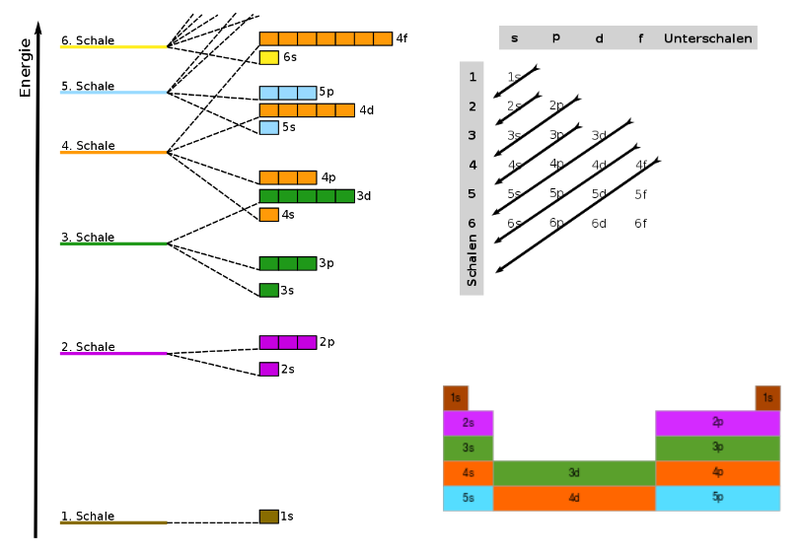
Energiestufen der Orbitale

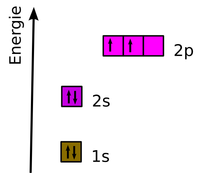
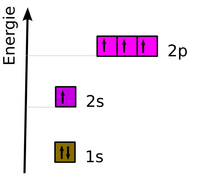
Beispiel für Elektronenkonfigurationen

Natrium

Mangan

Kupfer

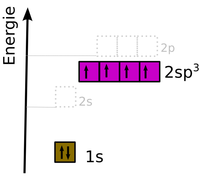
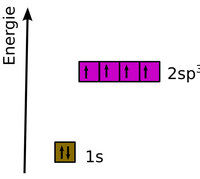
Hybridisierung

     

Orbital-Modell bei Mehrfachbindungen

• Doppelbindung beim Ethen - Seite mit Erklärungen und Übungen usw.
• Bindungsverhältnisse im Benzol

Weitere Beispiele für unterschiedlichen Hybridisierungen

• Propadien
• Ethin