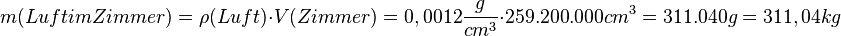Berechnungen mit der Dichte
Zur Erinnerung
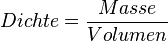 oder mit Symbolen oder mit Symbolen 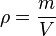 . .
|
Berechnung der Dichte
|
Bearbeite die Aufgaben 1 und 2 im Buch auf Seite 24. Auf Seite 25 findest du eine Tabelle mit den benötigten Dichte-Werten. Hinweis: Die Rechnungen habe ich sehr ausführlich aufgeschrieben. Auch wenn du es vielleicht für zu ausführlich hälst, solltest du doch bei jedem neuen Aufgabentyp mal mindestens eine Rechnung genauso ausführlich aufschreiben, damit man du im Heft bei Unsicherheiten noch einmal genau nachlesen kannst. |
| VERSUCH:
In der Schule bearbeiten wir die Experimente, wie sie auf den Arbeitsblättern der Seite http://www.Chemie-Master.de beschrieben sind. Die Arbeitsblätter zur Bestimmung der Dichte von Flüssigkeiten und zur Dichte von Feststoffen sind dort verfügbar. Als Flüssigkeiten stehen zur Verfügung:
Die unregelmäßigen Feststoffe sind zum Beispiel:
Das Ablesen von Skalen an den Meßzylindern könnt ihr in diesem Lückentext üben. |
Umrechnung von Größen
Nicht immer wird das Volumen in cm³ und die Masse in angegeben. Deshalb solltest du dich an einige Umrechnungsfaktoren erinnern. Im folgenden Kästchen gibt es eine Auswahl von wichtigen Einheiten und allgemein gültige Vorsilben. Alle Vorsilben findest du bei Bedarf auf Wikipedia auf der Seite ![]() Vorsätze für Maßeinheiten . Kennt man die Vorsilben, muss man bei den einzelnen Größen kaum noch etwas zusätzlich lernen.
So auch bei den Volumina, denn da muss man eigentlich nichts weiter lernen, außer die Umrechnung der Strecken. Die Volumina-Einheiten leiten sich ja von den Strecken-Einheiten ab. Denn man muss ja zum Beispiel beim Volumen von Quadern berechnen, indem man die Längen von Breite, Höhe und Länge multipliziert. Alles zusammen bekommst du in den
Vorsätze für Maßeinheiten . Kennt man die Vorsilben, muss man bei den einzelnen Größen kaum noch etwas zusätzlich lernen.
So auch bei den Volumina, denn da muss man eigentlich nichts weiter lernen, außer die Umrechnung der Strecken. Die Volumina-Einheiten leiten sich ja von den Strecken-Einheiten ab. Denn man muss ja zum Beispiel beim Volumen von Quadern berechnen, indem man die Längen von Breite, Höhe und Länge multipliziert. Alles zusammen bekommst du in den ![]() Filmen (1) und (2) erklärt.
Filmen (1) und (2) erklärt.
| Wichtige Umrechnungsfaktoren:
Allgemein gültige Vorsilben:
Massen:
Volumina:
|
|
Zum Üben und Testen deines Wissen zu den Einheiten gibt es ein paar kleine Quizze: ein Zuordnungsquiz, ... |
Rechnen mit der Dichte
Die Dichte kann man nicht nur bestimmen. Wenn sei bekannt ist kann man aus bekanntem Volumen das Gewicht berechnen oder umgekehrt, wenn das Gewicht bekannt ist, das Volumen der Stoffportion ausrechnen. Dazu muss man aber die Formel der Dichte 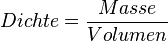 so umstellen, dass der jeweils gesuchte Wert alleine auf einer Seite steht. Mathematiker sagen dazu auch umformen. Wie das geht, bekommst du im
so umstellen, dass der jeweils gesuchte Wert alleine auf einer Seite steht. Mathematiker sagen dazu auch umformen. Wie das geht, bekommst du im ![]() Film gezeigt.
Film gezeigt.
|
Berechne die Aufgaben 3 und 4 im Buch auf Seite 24. Auf Seite 25 findest du eine Tabelle mit benötigten Werten. |
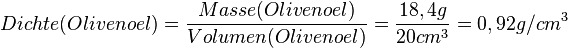
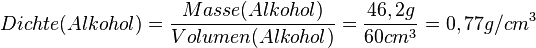

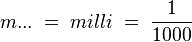 /
/ 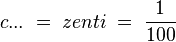 /
/ 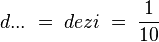
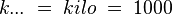
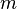 , Basiseinheit
, Basiseinheit 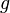 (Gramm),
(Gramm), 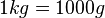 ,
, 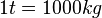
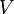 , Basiseinheit
, Basiseinheit 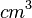 (Kubikzentimeter),
(Kubikzentimeter), 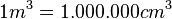 ,
, 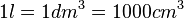
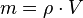 Rechnung:
Rechnung: 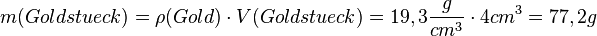
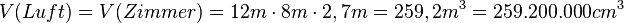 und
und